Xét các số thực với a ≠ 0 , b > 0 sao cho phương trình a x 3 - x 2 + b = 0 có ít nhất hai nghiệm thực. Giá trị lớn nhất của biểu thức a 2 b bằng
A. 4 27 .
B. 15 4 .
C. 27 4 .
D. 4 15 .
Xét các số thực với a ≠ 0 , b > 0 sao cho phương trình a x 3 - x 2 + b = 0 có ít nhất hai nghiệm thực. Giá trị lớn nhất của biểu thức a 2 b bằng
A. 4 27
B. 15 4
C. 27 4
D. 4 15
Xét phương trình a x 3 − x 2 + b x − 1 = 0 với a, b là các số thực, a ≠ 0 , a ≠ b sao cho các nghiệm đều là số thực dương. Tìm giá trị nhỏ nhất của biểu thức P = 5 a 2 − 3 a b + 2 a 2 b − a .
A. 15 3 .
B. 8 2 .
C. 11 6 .
D. 12 3 .
Xét phương trình ax3- x2+ bx-1=0 với a, b là các số thực a≠0; a≠ b sao cho các nghiệm đều là số thực dương. Tìm giá trị nhỏ nhất của biểu thức P = 5 a 2 - 3 a b + 2 a 2 ( b - a ) .
A. 15 3
B. 8 2
C. 11 6
D. 12 3
Giả sử phương trình đã cho có 3 nghiệm
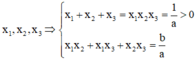
Khi đó
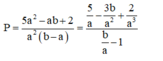
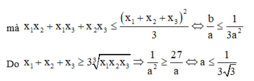
Suy ra
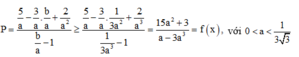
Xét hàm số:
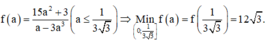
Chọn D.
trên tập hợp số phức,xét phương trình z2-4az+b2+2=0 (a,b là các tham số thực).Có bao nhiêu cặp số thực (a;b) sao cho phương trình đó có 2 nghiệm z1,z2 thoả mãn z1+2iz2=3+3i
Do \(z_1;z_2\) là 2 nghiệm của pt, đặt \(z_1=x+yi\Rightarrow z_2=x-yi\)
Theo Viet: \(\left\{{}\begin{matrix}z_1+z_2=2x=4a\\z_1z_2=x^2+y^2=b^2+2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=2a\\x^2+y^2=b^2+2\end{matrix}\right.\) (1)
\(z_1+2i.z_2=3+3i\Leftrightarrow x+yi+2i\left(x-iy\right)=3+3i\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+2y=3\\y+2x=3\end{matrix}\right.\) \(\Rightarrow x=y=1\)
Thế vào (1) \(\Rightarrow\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b=0\end{matrix}\right.\) \(\Rightarrow\) có 1 cặp số thực thỏa mãn
Cho a , b , c là các số thực phân biệt sao cho các phương trình : x2 + ax + 1 = 0 và x2 + bx + c = 0 có nghiệm chung đồng thời các phương trình x2 + x + a = 0 và x2 + cx + b = 0 cũng có nhgieemj chung . Hãy tìm tổng a + b + c
a) ax^2 + bx + c = 0
Để phương trình thỏa mãn điều kiện có 2 nghiệm dương phân biệt.
∆ > 0
=> b^2 - 4ac > 0
x1 + x2 = -b/a > 0
=> b và a trái dấu
x1.x2 = c/a > 0
=> c và a cùng dấu
Từ đó ta xét phương trình cx^2 + bx^2 + a = 0
∆ = b^2 - 4ac >0
x3 + x4 = -b/c, vì a và c cùng dấu mà b và a trái dấu nên b và c trái dấu , vì vậy -b/c >0
x3.x4 = a/c, vì a và c cùng dấu nên a/c > 0
=> phương trình cx^2 + cx + a có 2 nghiệm dương phân biệt x3 và x4
Vậy nếu phương trình ax^2 + bx + c = 0 có 2 nghiệm dương phân biệt thì phương trình cx^2 + bx + a = 0 cũng có 2 nghiệm dương phân biệt.
b) Ta có, vì x1, x2, x3, x4 không âm, dùng cô si.
x1 + x2 ≥ 2√( x1.x2 )
x3 + x4 ≥ 2√( x3x4 )
=> x1 + x2 + x3 + x4 ≥ 2[ √( x1.x2 ) + √( x3x4 ) ] (#)
Tiếp tục côsi cho 2 số không âm ta có
√( x1.x2 ) + √( x3x4 ) ≥ 2√[√( x1.x2 )( x3.x4 ) ] (##)
Theo a ta có
x1.x2 = c/a
x3.x4 = a/c
=> ( x1.x2 )( x3.x4 ) = 1
=> 2√[√( x1.x2 )( x3.x4 ) ] = 2
Từ (#) và (##) ta có đúng k bn
Trong không gian Oxyz, cho hình lập phương ABCD.A’B’C’D’ sao cho A ( 0;0;0 ); B( a;0;0 ); D ( 0;a;0 ); A' ( 0;0;a ). Xét các mệnh đề sau:(I): x + y + z - a = 0 là phương trình mặt phẳng (A’BD). (II): x + y + z - 2a = 0 là phương trình mặt phẳng (CB’D). Hãy chọn mệnh đề đúng.
A. Chỉ (I)
B. Chỉ (II)
C. Cả hai đều sai
D. Cả hai đều đúng
Thay các tọa độ B( a;0;0 ); D ( 0;a;0 ); A' ( 0;0;a ) vào phương trình ( I ) thấy thỏa mãn nên ( I ) đúng
Đáp án D
Nhờ các bạn giải dùm:
1/Cho 3 số thực phân biệt a, b, c sao cho phương trình x2+ax+1=0 và x2+bx+c=0 có nghiệm chung, đồng thời phương trình x2+x+a=0 và
x2+cx+b=0 cũng có nghiệm chung.
Hãy tính a+b+c
2/Tìm a, b, c nguyên dương sao cho: a2-2c+2=abc
Ý tưởng như sau:
\(x^2+ax+1=0\) và \(x^2+bx+c=0\) là 2 pt có nghiệm chung nên hệ pt sau có nghiệm (nhận xét quan trọng):
\(\hept{\begin{cases}x^2+ax+1=0\\x^2+bx+c=0\end{cases}}\Leftrightarrow\hept{\begin{cases}\left(a-b\right)x=c-1\\x^2+ax+1=0\end{cases}}\)
Do \(a\ne b\) nên thay \(x=\frac{c-1}{a-b}\) xuống pt dưới được: \(\left(\frac{c-1}{a-b}\right)^2+\frac{a\left(c-1\right)}{a-b}+1=0\)
Hay \(\left(c-1\right)^2+a\left(c-1\right)\left(a-b\right)+\left(a-b\right)^2=0\)
-----
\(x^2+x+a=0\) và \(x^2+cx+b=0\) có nghiệm chung thì hệ pt sau có nghiệm:
\(\hept{\begin{cases}x^2+x+a=0\\x^2+cx+b=0\end{cases}\Leftrightarrow\hept{\begin{cases}\left(c-1\right)x=a-b\\x^2+x+a=0\end{cases}}}\)
Do \(a\ne b\) nên \(c\ne1\), thay \(x=\frac{a-b}{c-1}\) xuống pt dưới được:
\(\left(\frac{a-b}{c-1}\right)^2+\frac{a-b}{c-1}+a=0\) hay \(\left(a-b\right)^2+\left(a-b\right)\left(c-1\right)+a\left(c-1\right)^2=0\)
-----
Đặt \(x=a-b,y=c-1\)
Ta có hệ: \(\hept{\begin{cases}x^2+axy+y^2=0\\x^2+xy+ay^2=0\end{cases}\Rightarrow\left(a-1\right)xy=\left(a-1\right)y^2}\)
Nhớ rằng \(a=1\) không xảy ra vì khi đó \(x^2+ax+1=0\) vô nghiệm.
Vậy \(a\ne1\), do \(y\ne0\) nên \(x=y\). Tức là \(a-b=c-1\).
Tới đây quay lại mấy cái nghiệm chung sẽ thấy các nghiệm chung đều là \(1\).
Mà như vậy thì \(b+c=-1,a=-2\) nên \(a+b+c=-4\)
Xét các số nguyên dương a,b sao cho phương trình a ln 2 x + b ln x + 5 = 0 có hai nghiệm phân biệt x 1 ; x 2 và phương trình 5 log 2 x + b log x + a = 0 có hai nghiệm phân biệt x 3 ; x 4 thỏa mãn x 1 x 2 > x 3 x 4 . Tìm giá trị nhỏ nhất S m i n của S = 2a+3b.
A. Smin = 25
B. Smin = 17
C. Smin = 30
D. Smin = 33
Cho các số thực a, b khác 0. Xét hàm số f ( x ) = a ( x + 1 ) 3 + b x e x với mọi x khác -1. Biết f'(0)=-22 và ∫ 0 1 f ( x ) d x = 5 . Tính a 2 + b 2 .
A. 42
B. 72
C. 68
D. 10