Gọi F ( x ) = ( a x 2 + b x + c ) e x là một nguyên hàm của hàm số f ( x ) = ( x - 1 ) 2 e x . Tính S= a+2b+c:
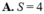
![]()
![]()
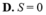
A gọi B bằng bác , B gọi C là ông nội ,C gọi D là cậu , D gọi E là gì ,E gọi F là chú , F gọi Z là con , Z gọi X là bố , X gọi V là cụ , V gọi M là chồng . hỏi A gọi M là gì .
Câu 1: Tìm x, biết:
a) (x+1) (2-x)-(5x+5) (x+2)=-4x^2+2
Câu 2: Cho tam giác ABC cân tại A (góc A>90°) có đường cao AD. Kẻ DH vuông góc AB (H thuộc AB) gọi E,F là hình chiếu vuông góc của H trên BC và AD. Gọi I là trung điểm của HD
a) Chứng minh: E, I, F thẳng hàng
b) Gọi G là điểm đối xứng của E qua D. Tứ giác DHFG là hình gì? Vì sao?
c) Chứng minh: AI vuông góc HC
Tính f(x)=\(\int e^2dx\), trong đó e là hằng số và e\(\approx\)2,718
A. f(x)= \(\dfrac{e^2x^2}{2}+C\)
B. f(x) =\(\dfrac{e^3}{3}+C\)
C. f(x) = e\(^2\)x+C
D. f(x) = 2ex + C
( Mu4-42. Cho hàm so $f(x)$ có đạo hàm trên đoạn $[0 ; 1]$ thỏa mãn $f(1)=0$ và $\int_0^1\left[f^{\prime}(x)\right]^2 d x=\int_0^1(x+1) e^x f(x) d x=\frac{e^2-1}{4}$. Tinh tich phân $I=\int_{0}^1 f(x) d x$.
A. $I=2-e$.
B. $I=\frac{e}{2}$.
C. $l=e-2$.
D. $1=\frac{e-1}{2}$
BT: Tìm nghiệm của đa thức
A. A(x)=4x-1. E. F(x)=5-x^2.
B. B(x)=2x^2-8. F. B(x)=(1/2-x)×(2x+1).
C. C(x)=x^2+1. G. C(x)=3x^2-x.
D. D(x)=(3x-2)×(2x-3). H. D(x)= 1/2x^2+x^3
GIÚP MK VS NHA
a) Đặt A(x)=0
\(\Leftrightarrow4x-1=0\)
\(\Leftrightarrow4x=1\)
hay \(x=\dfrac{1}{4}\)
b) Đặt B(x)=0
\(\Leftrightarrow2x^2-8=0\)
\(\Leftrightarrow2x^2=8\)
\(\Leftrightarrow x^2=4\)
hay \(x\in\left\{2;-2\right\}\)
c) Đặt C(x)=0
\(\Leftrightarrow x^2+1=0\)
mà \(x^2+1\ge1>0\forall x\)
nên \(x\in\varnothing\)
Tìm GTLN của biểu thức:
a) A= 5x- x^2
b) B= x- x^2
c) C= 4x- x^2+ 3
d) D= -x^2+ 6x- 11
e) E= 5- 8x- x^2
f) F= 4x- x^2+ 1
I : Tìm giá trị lớn nhất của biểu thức
a) A=5x-x^2 b) B=x-x^2 c) C= 4x-x^2+3
d) D=-x^2+6x-11 e) E=5-8x-x^2 f) F=4x-x^2+1
\(a.A=5x-x^2\)
\(=-\left(x^2-5x\right)=-\left[\left(x-\dfrac{5}{2}\right)^2+\dfrac{25}{4}\right]=-\left(x-\dfrac{5}{2}\right)^2+\dfrac{25}{4}\le\dfrac{25}{4}\)
\(\Rightarrow Max_A=\dfrac{25}{4}\) khi \(x=\dfrac{5}{2}\)
\(b.B=x-x^2=-\left(x^2-x\right)=-\left[\left(x-\dfrac{1}{2}\right)^2-\dfrac{1}{4}\right]=-\left(x-\dfrac{1}{2}\right)^2+\dfrac{1}{4}\le\dfrac{1}{4}\)
\(\Rightarrow Max_B=\dfrac{1}{4}\Leftrightarrow x=\dfrac{1}{2}\)
\(c.C=4x-x^2+3=-\left(x^2-4x-3\right)=-\left(x^2-4x+4-7\right)=-\left(x-2\right)^2+7\le7\)
\(\Rightarrow Max_C=7\Leftrightarrow x=2\)
a) Ta có:
\(A=5x-x^2\)
\(=-\left(x^2-5x\right)\)
\(=-\left(x^2-5x\right)-6,25+6,25\)
\(=-\left(x^2-5x+6,25\right)+6,25\)
\(=-\left(x-2,5\right)^2+6,25\)
Ta lại có:
\(\left(x-2,5\right)^2\ge0\)
\(\Rightarrow-\left(x-2,5\right)^2\le0\)
\(\Rightarrow-\left(x-2,5\right)^2+6,25\le6,25\)
\(\Rightarrow A\le6,25\)
Dấu "=" xảy ra \(\Leftrightarrow\left(x-2,5\right)^2=0\)
\(\Leftrightarrow x-2,5=0\)
\(\Leftrightarrow x=2,5\)
Vậy MaxA = 6,25 \(\Leftrightarrow x=2,5\)
\(d.D=-x^2+6x-11=-\left(x^2-6x+11\right)=-\left(x-3\right)^2-2\le-2\)
\(\Rightarrow Max_D=-2\Leftrightarrow x=3\)
\(e.E=5-8x-x^2=-\left(x^2+8x-5\right)=-\left[\left(x+4\right)^2-21\right]=-\left(x+4\right)^2+21\le21\)
\(\Rightarrow Max_E=21\Leftrightarrow x=-4\)
\(f.F=4x-x^2+1=-\left(x-4x-1\right)=-\left[\left(x-2\right)^2-5\right]=-\left(x-2\right)^2+5\le5\)
\(\Rightarrow Max_F=5\Leftrightarrow x=2\)
giúp em mấy bài nguyên hàm với ạ. huhu
1) cho f(x)=8sin bình(x+pi/12) một nguyên hàm F(x) của f(x) thỏa F(0)=8 là
A.4x+2sin(2x+pi/6)+9
B.4x-2sin(2x+pi/6)-9
C.4x+2sin(2x+pi/6)+7
D.4x-2sin(2x+pi/6)+7
2)cho f(x)=x*(e mũ -x) một nguyên hàm F(x) của f(x) thỏa F(0)=1 là
A.-(x+1) *(e mũ -x)+1
B.-(x+1)*(e mũ -x)+2
C.(x+1)*(e mũ -x)+1
D.(x+1)*(e mũ -x)+2
Lời giải:
Bài 1:
Ta nhớ công thức \(\sin^2x=\frac{1-\cos 2x}{2}\). Áp dụng vào bài toán:
\(F(x)=8\int \sin^2\left(x+\frac{\pi}{12}\right)dx=4\int \left [1-\cos \left(2x+\frac{\pi}{6}\right)\right]dx\)
\(\Leftrightarrow F(x)=4\int dx-4\int \cos \left(2x+\frac{\pi}{6}\right)dx=4x-2\int \cos (2x+\frac{\pi}{6})d(2x+\frac{\pi}{6})\)
\(\Leftrightarrow F(x)=4x-2\sin (2x+\frac{\pi}{6})+c\)
Giải thích 1 chút: \(d(2x+\frac{\pi}{6})=(2x+\frac{\pi}{6})'dx=2dx\)
Vì \(F(0)=8\Rightarrow -1+c=8\Rightarrow c=9\)
\(\Rightarrow F(x)=4x-2\sin (2x+\frac{\pi}{6})+9\)
Câu 2:
Áp dụng nguyên hàm từng phần như bài bạn đã đăng:
\(\Rightarrow F(x)=-xe^{-x}-e^{-x}+c\)
Vì \(F(0)=1\Rightarrow -1+c=1\Rightarrow c=2\)
\(\Rightarrow F(x)=-e^{-x}(x+1)+2\), tức B là đáp án đúng
Xác định giá trị a, b, c để hàm số F ( x ) = ( a x 2 + b x + c ) e - x là một nguyên hàm của f ( x ) = ( x 2 - 3 x + 2 ) e - x
A. a = -1; b = 1; c = -1
B. a = -1; b = -5; c = -7
C. a = 1; b = -3; c = 2
D. a = 1; b = -1; c = 1
Tìm x biết: a) (2-x).x2< hoặc = 0. b)(x-7).(x+3)<0. c) (x+4).(x+3)>0. d) (x2+4x).(5-x)<0. e) x/x+1>0. f) 2x-1/2-x< hoặc = 0. Bài 2: tìm giá trị nhỏ nhất của các biểu thức sau: a) A=x2+y2+2014. b) B=(x+30)2+(y-4)2+17 c)C=(y-9)2 + |x-3| -1. d) D=x4 +11. e) E=-2014/|x|+2015. f)F=|x|+214/215
a) Ta có: \(x^2\ge0\forall x\in Q\)
\(y^2\ge0\forall x\in Q\)
\(\Rightarrow x^2+y^2+2014\ge2014\forall x\in Q\)
Dấu giá trị nhỏ nhất của biểu thức là 2014, xảy ra khi \(\left\{{}\begin{matrix}x^2=0\\y^2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=0\end{matrix}\right.\)
b, Ta có: \(\left(x+30\right)^2\ge0\forall x\in Q\)
\(\left(y-4\right)^2\ge0\forall x\in Q\)
\(\Rightarrow\left(x+30\right)^2+\left(y-4\right)^2+17\ge17\forall x\in Q\)
Dấu giá trị nhỏ nhất của biểu thức là 17, xảy ra khi \(\left\{{}\begin{matrix}\left(x+30\right)^2=0\\\left(y-4\right)^2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-30\\y=4\end{matrix}\right.\)
c, Ta có: \(\left(y-9\right)^2\ge0\forall x\in Q\)
\(\left|x-3\right|\ge0\forall x\in Q\)
\(\Rightarrow\left(y-9\right)^2+\left|x-3\right|^2-1\ge-1\forall x\in Q\)
Dấu giá trị nhỏ nhất của biểu thức là -1 xảy ra khi \(\left\{{}\begin{matrix}\left(y-9\right)^2=0\\\left|x-3\right|=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=9\\x=3\end{matrix}\right.\)
a) \(\left(2-x\right)x^2\le0\)
Ta có: \(\left(2-x\right)x^2=0\Leftrightarrow\left[{}\begin{matrix}x^2=0\\2-x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
Vì \(x^2\ge0\Rightarrow\left(2-x\right)x^2\Leftrightarrow2-x< 0\Leftrightarrow2< x\)
Vậy ......
b, \(\left(x-7\right)\left(x+3\right)< 0\Leftrightarrow\left[{}\begin{matrix}x-7< 0\\x+3< 0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x< 7\\x< -3\end{matrix}\right.\)
Vây........
c, \(\left(x+4\right)\left(x+3\right)\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x+4>0\\x+3>0\end{matrix}\right.\\\left\{{}\begin{matrix}x+4< 0\\x+3< 0\end{matrix}\right.\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x>-4\\x>-3\end{matrix}\right.\\\left\{{}\begin{matrix}x< -4\\x< -3\end{matrix}\right.\end{matrix}\right.\)
Vậy..............