Đáp án D

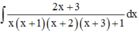
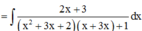
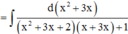
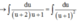
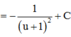
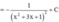
Suy ra tổng của các nghiệm của phương trình g(x) = 0 là  - 3

Đáp án D

Bài 1:

Với $x_1,x_2$ là hai nghiệm của phương trình đã cho, ta áp dụng hệ thức Viete có: \(\left\{\begin{matrix} x_1+x_2=2(m-1)\\ x_1x_2=m^2-1\end{matrix}\right.\)

\(\Rightarrow \left\{\begin{matrix} x_1+x_2+2=2m\\ x_1x_2+1=m^2\end{matrix}\right.\)\(\Rightarrow \left\{\begin{matrix} (x_1+x_2+2)^2=4m^2\\ 4(x_1x_2+1)=4m^2\end{matrix}\right.\)

\(\Rightarrow (x_1+x_2+2)^2=4(x_1x_2+1)\)

\(\Leftrightarrow x_1^2+x_2^2+2x_1x_2+4(x_1+x_2)+4=4x_1x_2+4\)

\(\Leftrightarrow x_1^2+x_2^2-2x_1x_2+4(x_1+x_2)=0\)

Đây chính là hệ thức cần tìm

Bài 2:

Áp dụng hệ thức Viete ta có: \(\left\{\begin{matrix} x_1+x_2=2(m-1)\\ x_1x_2=m^2-3m\end{matrix}\right.\)

\(\Rightarrow \left\{\begin{matrix} x_1+x_2+2=2m(1)\\ x_1x_2=m^2-3m\end{matrix}\right.\)

\(\Rightarrow \left\{\begin{matrix} (x_1+x_2+2)^2=4m^2\\ 4x_1x_2=4m^2-12m\end{matrix}\right.\) \(\Rightarrow 12m=(x_1+x_2+2)^2-4x_1x_2(2)\)

Từ \((1); (2)\Rightarrow (x_1+x_2+2)^2-4x_1x_2=6(x_1+x_2+2)\)

\(\Leftrightarrow x_1^2+x_2^2-2x_1x_2-2(x_1+x_2)-8=0\)

Đây chính là biểu thức cần tìm.

1) -Của Tố Hữu

-Bài thơ " Lượm " được tác giả Tố Hữu sáng tác vào năm 1949 khi cuộc kháng chiến chống thực dân Pháp đang ở giai đoạn vô cùng ác liệt.

2) PTBĐ:Biểu cảm kết hợp với tự sự và miêu tả.

3)Trong bài thơ, tác giả đã gọi chú bé Lượm bằng những từ:Cháu,Chú bé,Lượm,Chú đồng chí

=>Thân thiết,gắn bó,yêu mến

4)Những từ láy loát choắt, xinh xinh, thoăn thoát, nghênh nghềnh được dùng rất gợi hình gợi cảm, cùng với thể thơ bốn chữ và nhịp thơ nhanh, tạo âm hưởng vui tươi, nhí nhảnh rất phù hợp với một chú bé như Lượm

Nhiệt tỏa ra khi hình thành 1 mol Na₂O(s) ở điều kiện chuẩn từ phản ứng giữa Na(s) và O₃(g) không được coi là nhiệt tạo thành chuẩn của Na₂O(s) vì oxygen dạng phân tử O₃ (ozone) không là dạng bền nhất.

C + O₂ -> CO₂ (1)

4P + 5O₂ -> 2P₂O₅ (2)

Gọi m_C là x(g) (0<x<3) => n_C = x/12 (mol)

Thì m_P là 3-x (g) => n_P = (3-x)/31 (mol)

n_O2 = 1,68/22,4 = 0,075 (mol)

Theo PT (1) ta có: n_O2 = n_C = x/12 (mol)

Theo PT (2) ta có: n_O2 = 5/4n_P = (5/4).[(3-x)/31] = (3-x)/24,8 (mol)

Theo đề bài, n_O2 là 0,075 mol nên ta có:

x/12 + (3-x)/24,8 = 0,075 <=> x = 1,4625 (g)

=> m_C là 1,4625 gam

Do đó: %C = (1,4625/3).100% = 48,75%

%P = 100% - 48,75% = 51,25%

a: Xét ΔCAE vuông tại A và ΔCKE vuông tại K có

CE chung

góc ACE=góc KCE

Do đó: ΔCAE=ΔCKE

Suy ra: CA=CK

Xét ΔEAB có góc EBC=góc ECB

nên ΔEAB cân tại E

mà EK là đường cao

nên K là trung điểm của CB

=>CK=KB=CA

b: Ta có: CA=CK

EA=EK

DO đó: CE là đường trung trực của AK