Hệ số của số hạng chứa x 5 trong khai triển thành đa thức của ( 1 + x ) 10 ( 1 + x 2 ) 12 là
A. 816.
B. 5920.
C. 379984.
D. 2352.
Cho biểu thức: P(x) = ( 1 + x ) 9 + ( 1 + x ) 10 + ( 1 + x ) 11 + ( 1 + x ) 12 + ( 1 + x ) 13 + ( 1 + x ) 14 + ( 1 + x ) 15 . Hệ số của số hạng chứa x 9 trong khai triển thành đa thức của P(x) là
A. 3003
B. 8000
C. 8008
D. 3000
Chọn C
Ta có: 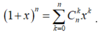 .
.
Số hạng tổng quát của khai triển là: ![]() . Hệ số của
x
k
trong khai triển là:
C
n
k
. Hệ số của
x
k
trong khai triển là:
C
n
k
Hệ số của số hạng chứa x 9 trong biểu thức P(x) là:
![]() .
.
Tìm hệ số của số hạng chứa \(x^5\) trong khai triển đa thức \(f\left(x\right)=x\left(1-2x\right)^5\)
Ta có: \(x.\left(C^k_n.a^{n-k}.b^k\right)=x.\left(C^k_5.a^{5-k}.b^k\right)=C^k_5.1^{5-k}.2^k.x^k.x\)
\(=C^k_5.2^k.x^{k+1}\)
Mà ta cần tìm số hạng của x5
\(\Rightarrow k+1=5\Leftrightarrow k=4\)
Vậy số hạng của x5 là: \(C^4_5.2^4=80\)
Ta nhân thêm ''x'' vào số hạng tổng quát vì có ''x'' là nhân tử chung của mỗi số hạng trong khải triển
Tìm hệ số của số hạng chứa \(x^5\) trong khai triển của đa thức: \(\left(x+2\right)^7\)
Số hạng tổng quát của khai triển: \(C_7^k.x^k.2^{7-k}\)
Số hạng chứa \(x^5\Leftrightarrow k=5\)
Hệ số của số hạng đó là: \(C_7^5.2^2=...\)
Hệ số của số hạng chứa x 3 trong khai triển thành đa thức của biểu thức A = 1 − x 10 là
A. 30
B. -120
C. 120
D. -30
Hệ số của số hạng chứa x 3 trong khai triển thành đa thức của biểu thức A= 1 - x 10 là:
A. 30
B. -120
C. 120
D. -30
a.Tìm hệ số của số hạng chứa \(x^6\) trong khai triển \(\left(1+x^2\right)^{12}\)
b.Tìm hệ số của số hạng chứa \(x^6\) trong khai triển \(\left(2x-1\right)^{10}\)
HELP ME!
Tìm hệ số của số hạng chứa \(x^5\) trong khai triển \(\left(3x^3+3x^2+x+1\right)^{10}\) thành đa thức
\(=\left(3x^2+1\right)^{10}\left(x+1\right)^{10}\)
Do tất cả các số hạng chứa x trong khai triển \(\left(3x^2+1\right)^{10}\) đều mũ chẵn và số hạng tự do duy nhất bằng 1
\(\Rightarrow\) Hệ số của số hạng chứa \(x^5\) bằng hệ số của số hạng chứa \(x^5\) trong khai triển \(\left(x+1\right)^{10}\)
Theo khai triển nhị thức Newton thì hệ số này bằng 252
Bài 1:
a.Tìm hệ số của số hạng chứa \(x^6\) trong khai triển \(\left(1+x^2\right)^{12}\)
b.Tìm hệ số của số hạng chứa \(x^6\) trong khai triển \(\left(2x-1\right)^{10}\)
Giúp mk vs ạ!!!
Tìm hệ số lớn nhất trong các hệ số của các số hạng khi khai triển nhị thức sau thành đa thức (1+x)101
Giúp với ạ
Hệ số lớn nhất sẽ tương ứng với số hạng đứng chính giữa
=>Hệ số lớn nhất là \(C^{51}_{101}\)