Cho biết hàm số f ( x ) = x 3 - 3 x 2 + 2 x x ( x - 2 ) k h i x ( x - 2 ) ≠ 0 a k h i x = 0 liên tục trên R. Tính T = a 2 + b 2 .
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Hàm số f(x) có đạo hàm trên là hàm số f'(x). Biết đồ thị hàm số f'(x) được cho như hình vẽ. Hàm số f(x) nghịch biến trên khoảng
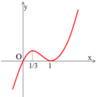
A. 0 ; + ∞
B. 1 3 ; 1
C. − ∞ ; 1 3
D. − ∞ ; 0
Đáp án D
f ' x < 0 ⇔ x < 0 do đó hàm số nghịch biến trên − ∞ ; 0
Bài 1 : Cho hàm số: y= f(x)= a.x2+b.x+c cho biết f(0)=2010, f(1)=2011, f(-1)=2012, Tính f(-2).
Bài 2 : Cho hàm số: y= f(x)= a.x2+b.x+c cho biết f(0)=2010, f(1)=2011, f(-1)=2012, Tính f(-2).
Bài 3 : Cho hàm số: y= f(x)= a.x2+b.x+c cho biết f(0)=2010, f(1)=2011, f(-1)=2012, Tính f(-2).
Bài 4 : Cho đa thức: f(x)= x2-a.x-3 và g(x)= (x3-x2-x-a-1)2015
a, Tìm a biết -1 là 1 nghiệm của f(x)
b, Với a tìm được ở câu a, Tìm nghiệm còn lại của f(x) và tính g(2).
Bài 5: Cho hàm số y= f(x)= a.x2+b.x+c và biết f(0)=2014, f(1)=2015, f(-1)=2017 ,
Tính f(-2).
Mọi người giúp mình với ạ mình đang cần gấp. Mình cảm ơn mọi người nhiều.
Bài 1 : làm tương tự với bài 2;3 nhé
Ta có : \(f\left(0\right)=c=2010;f\left(1\right)=a+b+c=2011\)
\(\Rightarrow f\left(1\right)=a+b=1\)
\(f\left(-1\right)=a-b+c=2012\Rightarrow f\left(-1\right)=a-b=2\)
\(\Rightarrow a+b=1;a-b=2\Rightarrow2a=3\Leftrightarrow a=\dfrac{3}{2};b=\dfrac{3}{2}-2=-\dfrac{1}{2}\)
Vậy \(f\left(-2\right)=4a-2b+c=\dfrac{4.3}{2}-2\left(-\dfrac{1}{2}\right)+2010=6+1+2010=2017\)
Cho biết hàm số f(x) có đạo hàm f'(x) liên tục và có một nguyên hàm là hàm số F(x). Tìm nguyên hàm
![]()
![]()
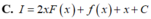
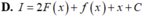
Hàm số f(x) có đạo hàm trên R là hàm số f’(x). Biết đồ thị hàm số f’(x)được cho như hình vẽ bên. Hàm số f(x) nghịch biến trên khoảng nào dưới đây?

A. − ∞ ; 0
B. 0 ; + ∞
C. − ∞ ; 1 3
D. 1 3 ; 1
Hàm số f (x) có đạo hàm trên ℝ là hàm số f '(x). Biết đồ thị hàm số f '(x) được cho như hình vẽ bên. Hàm số f (x) nghịch biến trên khoảng nào dưới đây?
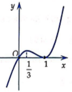
A. - ∞ ; 0
B. 0 ; + ∞
C. - ∞ ; 1 3
D. 1 3 ; 1
Cho hàm số y= f(x) . Biết f(x) có đạo hàm f’(x) và hàm số y= f’(x) có đồ thị như hình vẽ.

Hàm số g( x) = f(x- 1) đạt cực đại tại điểm nào dưới đây?
A. x= 2
B. x= 4
C . x= 3
D. x= 1
Chọn B
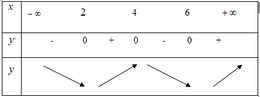
+ Dựa vào đồ thị hàm số ta thấy :
- Hàm số y= f( x) nghịch biến trên khoảng ( - ∞; 1) và ( 3; 5) .
- Hàm số y= f( x) nghịch biến trên khoảng ( 1 ; 3) và ( 5 ; + ∞)
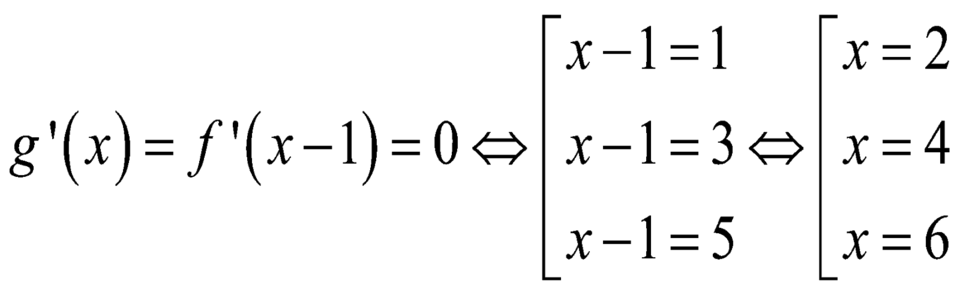
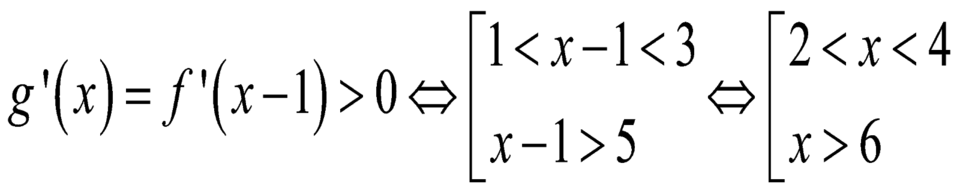
Cho biết hàm số f(x) có đạo hàm f’(x) liên tục và có một nguyên hàm là hàm số F(x). Tìm nguyên hàm I = ∫ 2 f x + f ' x + 1 d x
A. I=2F(x)+xf(x)+C
B. I=2xF(x)+x+1
C. I=2xF(x)+f(x)+x+C
D. I=2F(x)+f(x)+x+C
Cho hàm số y=f(x) biết hàm số f(x)có đạo hàm f'(x) và hàm số y=f'(x) có đồ thị như hình vẽ. Đặt g(x0=f(x+1) Kết luận nào sau đây là đúng?
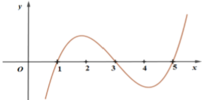
A. Hàm số g(x) đồng biến trên khoảng (3;4)
B. Hàm số g(x) đồng biến trên khoảng (0;1)
C. Hàm số g(x) nghịch biến trên khoảng (4;6)
D. Hàm số g(x) nghịch biến trên khoảng ( 2 ; + ∞ )
Cho hàm số y=f(x). Hàm số f'(x) có đồ thị như hĩnh vẽ bên:. Biết f(0) = -4, tìm số điể cực đại của hàm số y= 2.f (f(x)) - [ f(x)]2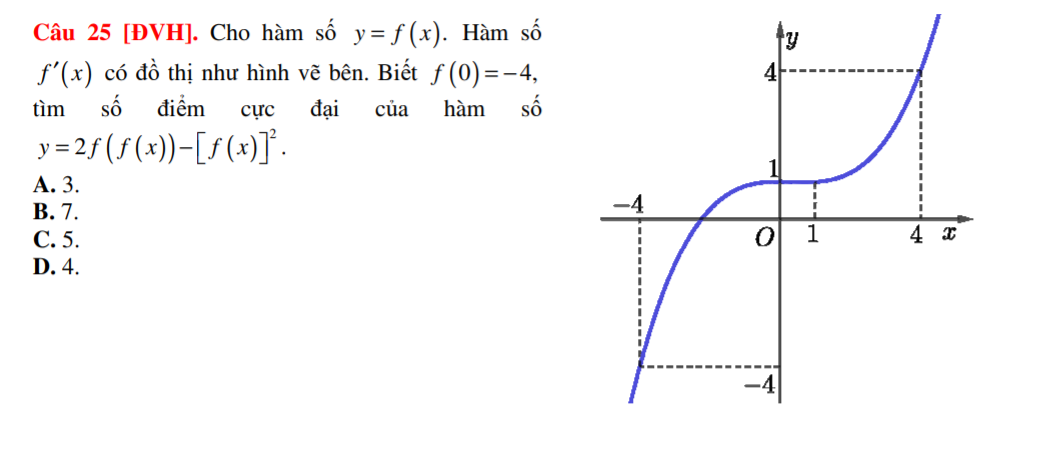
\(y'=2f'\left(x\right).f'\left(f\left(x\right)\right)-2f'\left(x\right).f\left(x\right)\)
\(y'=0\Rightarrow\left[{}\begin{matrix}f'\left(x\right)=0\\f'\left(f\left(x\right)\right)=f\left(x\right)\end{matrix}\right.\)
Từ đồ thị ta có \(f'\left(x\right)=0\Rightarrow x=x_1\) với \(-4< x_1< 0\)
Xét phương trình \(f'\left(f\left(x\right)\right)=f\left(x\right)\), đặt \(f\left(x\right)=t\Rightarrow f'\left(t\right)=t\)
Vẽ đường thẳng \(y=t\) (màu đỏ) lên cùng đồ thị \(y=f'\left(t\right)\) như hình vẽ:
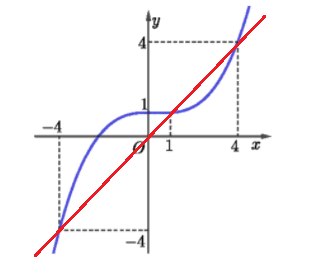
Ta thấy 2 đồ thị cắt nhau tại 3 điểm: \(t=\left\{-4;1;4\right\}\)
\(\Rightarrow\left[{}\begin{matrix}f\left(x\right)=-4\\f\left(x\right)=1\\f\left(x\right)=4\end{matrix}\right.\) (1)
Mặt khác từ đồ thị \(f'\left(x\right)\) và \(f\left(0\right)=-4\) ta được BBT của \(f\left(x\right)\) có dạng:
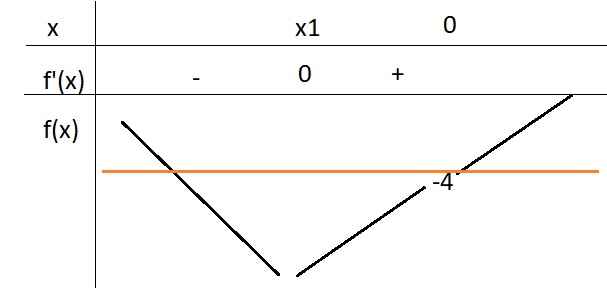
Từ đó ta thấy các đường thẳng \(y=k\ge-4\) luôn cắt \(y=f\left(x\right)\) tại 2 điểm phân biệt
\(\Rightarrow\) Hệ (1) có 6 nghiệm phân biệt (trong đó 3 nghiệm nhỏ hơn \(x_1\) và 3 nghiệm lớn hơn \(x_1\))
Từ đó ta có dấu của y' như sau:

Có 3 lần y' đổi dấu từ dương sang âm nên hàm có 3 cực đại
Cho hàm số y=f(x). Biết rằng hàm số f(x) có đạo hàm là f’(x) và hàm số y=f’(x) có đồ thị như hình vẽ bên. Khẳng định nào sau đây sai?
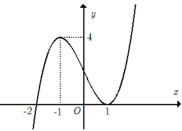
A. Hàm f(x) nghịch biến trên khoảng ( - ∞ ; - 2 )
B. Hàm f(x) đồng biến trên khoảng ( 1 ; + ∞ )
C. Trên (-1;1) thì hàm số f(x) luôn tăng.
D. Hàm f(x) giảm trên đoạn có độ dài bằng 2.