Chứng minh rằng với mọi góc a (0o ≤ a ≤ 180o) ta đều có cos2+ sin2α = 1.
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
PB
Những câu hỏi liên quan
chứng minh rằng với mọi góc x ( 0o ≤ x ≤ 90o), ta đều có
a) sin x = \(\sqrt{1-cos^{2_{ }}x}\)
b) cos x = \(\sqrt{1-sin^{2_{ }}x}\)
a: \(sin^2x+cos^2x=1\)
=>\(sin^2x=1-cos^2x\)
=>\(sinx=\sqrt{1-cos^2x}\)
b: \(sin^2x+cos^2x=1\)
=>\(cos^2x=1-sin^2x\)
=>\(cosx=\sqrt{1-sin^2x}\)
Đúng 2
Bình luận (0)
chứng minh rằng với mọi góc x ( 0o ≤ x ≤ 90o), ta đều có
a) tan2x = \(\dfrac{sin^{2_{ }}x}{cos^{2_{ }}x}\) ( x≠90o)
b) cot2x = \(\dfrac{cos^2x}{sin^2x}\) ( x ≠ 0o)
a: Ta sẽ có hình vẽ sau:
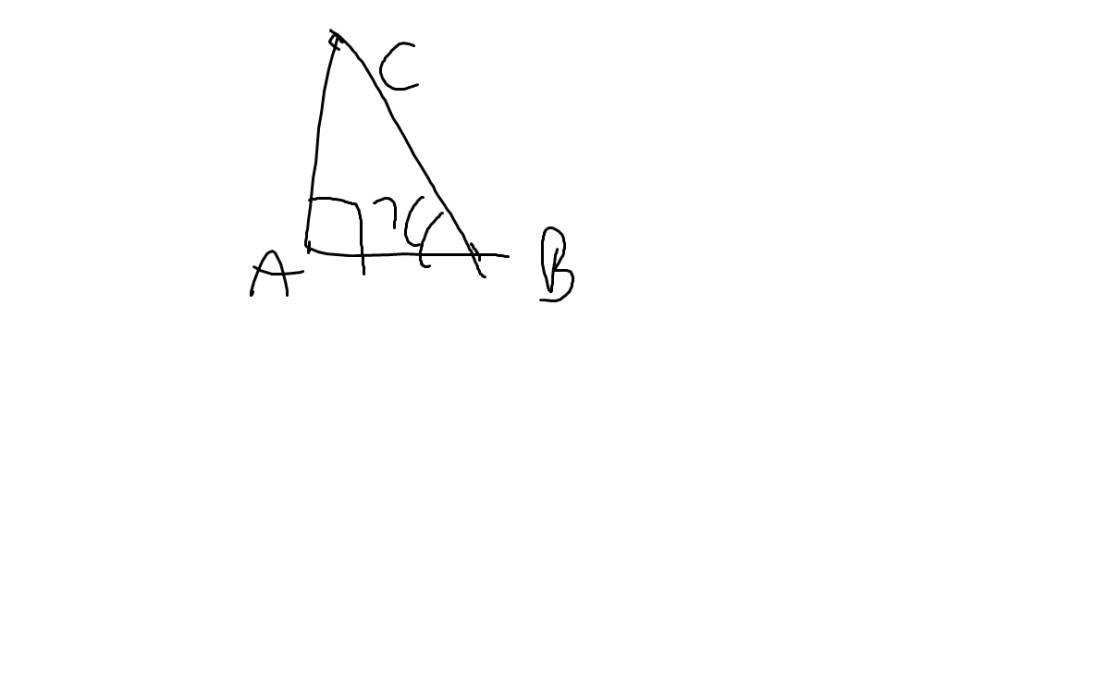
Đặt \(x=\widehat{B}\)
sin x=sin B=AC/BC
cosx=cosB=AB/BC
\(tanx=tanB=\dfrac{AC}{AB}=\dfrac{sinx}{cosx}\)
=>\(tan^2x=\dfrac{sin^2x}{cos^2x}\)
b: \(cot^2x=\dfrac{1}{tan^2x}=1:\dfrac{sin^2x}{cos^2x}=\dfrac{cos^2x}{sin^2x}\)
Đúng 2
Bình luận (0)
Sử dụng định nghĩa các tỉ số lượng giác của một góc nhọn để chứng minh rằng. Với góc nhọn α tùy ý, ta có: sin 2 α + cos 2 α = 1
Áp dụng định lí pitago trong tam giác vuông OAB có:
OB2 = OA2 + AB2
Từ đó ta có:
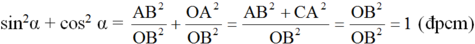
Đúng 0
Bình luận (0)
Sử dụng định nghĩa các tỉ số lượng giác của một góc nhọn để chứng minh rằng. Với góc nhọn α tùy ý, ta có:
a
)
tg
α
sin
α
cos
α
,
cotg
α
cos...
Đọc tiếp
Sử dụng định nghĩa các tỉ số lượng giác của một góc nhọn để chứng minh rằng. Với góc nhọn α tùy ý, ta có:
a ) tg α = sin α cos α , cotg α = cos α sin α tg α ⋅ cotg α = 1 b ) sin 2 α + cos 2 α = 1
Gợi ý: Sử dụng định lí Pitago.
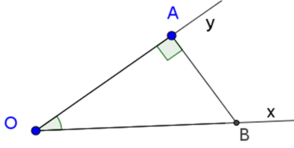
Dựng góc nhọn ∠xOy = α tùy ý.
Trên tia Ox lấy điểm B bất kì, kẻ BA ⊥ Oy (A ∈ Oy)
Theo định nghĩa tỉ số lượng giác của góc nhọn, ta có:

b) Áp dụng định lí pitago trong tam giác vuông OAB có:
O B 2 = O A 2 + A B 2
Từ đó ta có:
![]()
Đúng 0
Bình luận (0)
Chiếu một tia sáng vuông góc với một mặt gương phẳng. Góc phản xạ r có giá trị nào sau đây?
A. r = 90o
B. r = 45o
C. r = 180o
D. r = 0o
Đáp án: D
Vì khi chiếu tia tới vuông góc một mặt phẳng gương, tia tới trùng với pháp tuyển, góc tới bằng góc phản xạ bằng 0.
Đúng 0
Bình luận (0)
Nhắc lại khái niệm giá trị lượng giác của góc α, 0o ≤ α ≤ 180o.
Ta có thể mở rộng khái niệm giá trị lượng giác cho các cung và góc lượng giác.
Các số sinα; cosα; tanα; cotα được gọi là giá trị lượng giác của góc α, với 0o ≤ α ≤ 180o.
Đúng 0
Bình luận (0)
Với hai góc kề bù ta có định lý sau: Hai tia phân giác của hai góc kề bù tạo thành một góc vuôngHãy điền vào chỗ trống và sắp xếp bốn câu sau đây một cách hợp lí để chứng minh định lí trên.∠(tOy) (1/2). mo vì…∠(tOy) (1/2 )(180o - mo)vì…∠(tOt) 90o vì…∠(xOy) (180o - mo) vì…
Đọc tiếp
Với hai góc kề bù ta có định lý sau: Hai tia phân giác của hai góc kề bù tạo thành một góc vuông
Hãy điền vào chỗ trống và sắp xếp bốn câu sau đây một cách hợp lí để chứng minh định lí trên.
∠(tOy) = (1/2). mo vì…
∠(t'Oy) = (1/2 )(180o - mo)vì…
∠(tOt') = 90o vì…
∠(x'Oy) = (180o - mo) vì…
Chứng minh:
1) ∠tOy = 1/2. ∠xOy = 1/2. mo (Vì Ot là tia phân giác của góc xOy)
4) ∠x'Oy = 180o - ∠xOy = 180o - mo (Vì ∠x'Oy và ∠xOy kề bù)
2) ⇒ ∠t'Oy = 1/2. ∠x'Oy = 1/2. (180o - mo) (Vì Ot’ là phân giác của ∠x'Oy)
3) ⇒ ∠tOt' = ∠tOy + ∠t'Oy = 1/2. mo + 1/2. (180o - mo) = 90o.
Kết luận: Vậy hai tia phân giác của hai góc kề bù tạo thành góc vuông.
Đúng 1
Bình luận (0)
chứng minh rằng với mọi số tự nhiên n ta đều có: A= n4+6n3+11n2+6n chia hết cho 24
hỏi từ lâu hổng ai trả lời hihi
1. Cho hàm số f(x) xác định với mọi x thuộc R. Biết rằng với mọi x ta đều có:
f(x) + 3 . f( 1/x ) = x2. Tính f(2)
2.Cho tam giác ABC có độ dài 3 cạnh là BC = a; AC = b; AB = c thỏa mãn a2 + b2 > 5c2. Chứng minh rằng góc C < 60 độ.
câu 1 thôi nhé
f(x)+ 3. f(1/x) = \(^{x^2}\) (1)
f(1/x)+3. f(x)=\(\left(\frac{1}{x}\right)^2\)
3.f(1/x)+9.f(x)=\(\frac{3}{x^2}\) (2)
lấy (1)- (2)
-8. f(x)=\(\frac{x^4-3}{x^2}\)
f(x)= \(\frac{x^4-3}{-8.x^2}\)
thay vào tính được f(2)=\(\frac{-13}{32}\)
Đúng 0
Bình luận (0)



