a: Ta sẽ có hình vẽ sau:
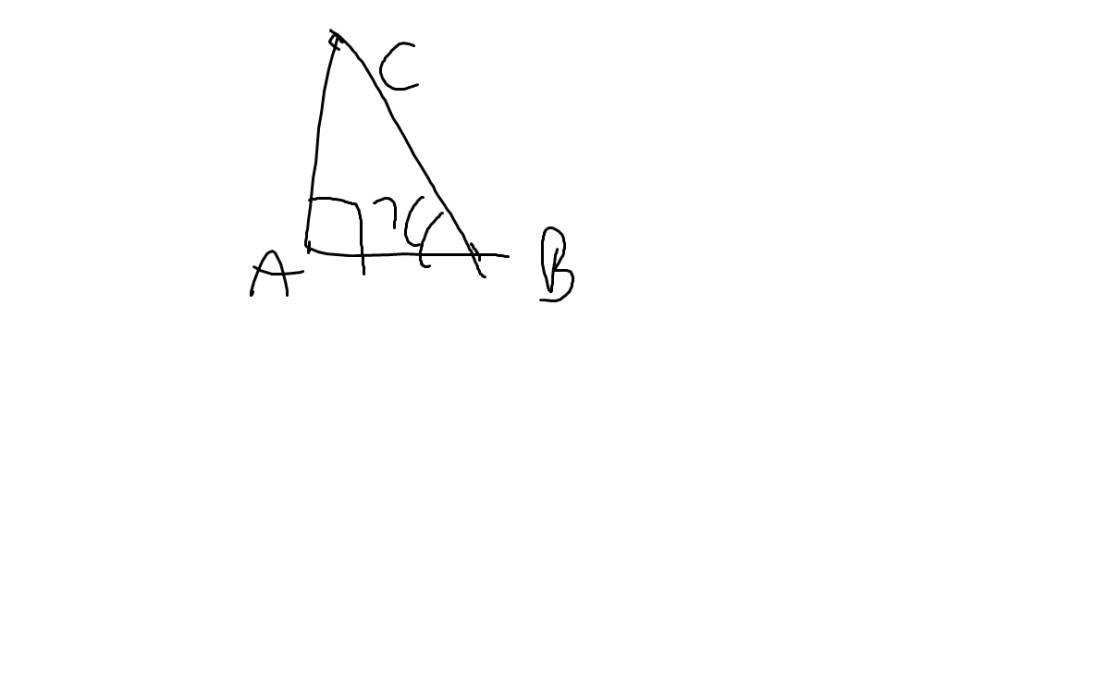
Đặt \(x=\widehat{B}\)
sin x=sin B=AC/BC
cosx=cosB=AB/BC
\(tanx=tanB=\dfrac{AC}{AB}=\dfrac{sinx}{cosx}\)
=>\(tan^2x=\dfrac{sin^2x}{cos^2x}\)
b: \(cot^2x=\dfrac{1}{tan^2x}=1:\dfrac{sin^2x}{cos^2x}=\dfrac{cos^2x}{sin^2x}\)
a: Ta sẽ có hình vẽ sau:

Đặt \(x=\widehat{B}\)
sin x=sin B=AC/BC
cosx=cosB=AB/BC
\(tanx=tanB=\dfrac{AC}{AB}=\dfrac{sinx}{cosx}\)
=>\(tan^2x=\dfrac{sin^2x}{cos^2x}\)
b: \(cot^2x=\dfrac{1}{tan^2x}=1:\dfrac{sin^2x}{cos^2x}=\dfrac{cos^2x}{sin^2x}\)
chứng minh rằng với mọi góc x ( 0o ≤ x ≤ 90o), ta đều có
a) sin x = \(\sqrt{1-cos^{2_{ }}x}\)
b) cos x = \(\sqrt{1-sin^{2_{ }}x}\)
Cho góc x với cos x = \(-\dfrac{1}{2}\). Tính giá trị của biểu thức S= \(4\sin^{2_{ }}\)x + 8 tan2 x.
Giải các pt
a) \(\sqrt{2}\sin\left(2x+\dfrac{\pi}{4}\right)=3\sin x+\cos x+2\)
b) \(\dfrac{\left(2-\sqrt{3}\right)\cos x-2\sin^2\left(\dfrac{x}{2}-\dfrac{\pi}{4}\right)}{2\cos x-1}=1\)
c) \(2\sqrt{2}\cos\left(\dfrac{5\pi}{12}-x\right)\sin x=1\)
Rúi gọn biểu thức :
\(A=\dfrac{\cos\left(x\right)+\cos\left(2x\right)+\cos\left(3x\right)}{\sin\left(x\right)+\sin\left(2x\right)+\sin\left(3x\right)}\)
\(\dfrac{sinx+cosx}{sinx}=\dfrac{sinx+cos^2\dfrac{x}{2}-sin^2\dfrac{x}{2}}{2cos\dfrac{x}{2}sin\dfrac{x}{2}}\)
\(0< x< 90\), chứng minh
CMR:
a, \(\frac{\cot^2x-\sin^2x}{\cot^2x-tan^2x}=sin^2x.\cos^2x\)
b, \(\frac{\tan x}{1-\tan^2x}.\frac{\cot^2-1}{\cot x}=1\)
c, \(\frac{1+\sin x.\cos x}{\sin^2x-\cos^2x}=\frac{\tan x+1}{\cot x+1}\)
d, \(\frac{\sin x+\cos x-1}{\sin x-cosx+1}=\frac{\cos x}{1+sinx}\)
Cho \(\cos2x=\dfrac{1}{2}\). Tính giá trị biểu thức:
\(P=\sin^22x-4\left(sin\dfrac{x}{2}.cos^5\dfrac{x}{2}-sin^5\dfrac{x}{2}.cos\dfrac{x}{2}\right)^2\)
Help me!!!!! plsssss
cho mình hỏi: chứng minh đẳng thức này: \(\sin^2x\left(1+\cot x\right)x+\cos^2\left(1+\tan x\right)=\left(\sin x+\cos x\right)^2\)có thể giải bằng cách lấy VT - VP = 0 có dc ko và tại sao ?
chứng minh đẳng thức này \(\frac{\sin x+\cos x-1}{\sin x-\cos x+1}=\frac{\cos x}{1+\sin x}\) có thể quy đồng rồi lấy VT - VP = 0 có dc ko và tại sao ?
Thanks nhiều
Rút gọn biểu thức A= sin x + sin 2 x + sin 3 x cos x + cos 2 x + cos 3 x
A. tan4x
B. tan 3x
C. tan 2x
D. tan x + tan 2x