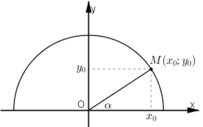
Vẽ đường tròn lượng giác (O; 1).
Với mọi α (0º ≤ α ≤ 180º) ta đều có điểm M(x0; y0) thuộc nửa đường tròn sao cho 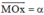
Khi đó ta có: sin α = y0 ; cos α = x0.
Mà M thuộc đường tròn lượng giác nên x02 + y02 = OM2 = 1⇒ sin2 α + cos2 α = 1.
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6

Vẽ đường tròn lượng giác (O; 1).
Với mọi α (0º ≤ α ≤ 180º) ta đều có điểm M(x0; y0) thuộc nửa đường tròn sao cho 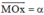
Khi đó ta có: sin α = y0 ; cos α = x0.
Mà M thuộc đường tròn lượng giác nên x02 + y02 = OM2 = 1⇒ sin2 α + cos2 α = 1.
chứng minh rằng với mọi góc x ( 0o ≤ x ≤ 90o), ta đều có
a) sin x = \(\sqrt{1-cos^{2_{ }}x}\)
b) cos x = \(\sqrt{1-sin^{2_{ }}x}\)
chứng minh rằng với mọi góc x ( 0o ≤ x ≤ 90o), ta đều có
a) tan2x = \(\dfrac{sin^{2_{ }}x}{cos^{2_{ }}x}\) ( x≠90o)
b) cot2x = \(\dfrac{cos^2x}{sin^2x}\) ( x ≠ 0o)
Nhắc lại khái niệm giá trị lượng giác của góc α, 0o ≤ α ≤ 180o.
Ta có thể mở rộng khái niệm giá trị lượng giác cho các cung và góc lượng giác.
Chứng minh rằng trong mọi tam giác ABC ta đều có:
a, a = b cosC + c cosB;
b, sinA = sinBcosC + sinCcosB;
c, ha = 2RsinBsinC.
Hãy nhắc lại định nghĩa giá trị lượng giác của một góc α với 0o ≤ α ≤ 180o. Tại sao khi α là các góc nhọn thì giá trị lượng giác này lại chính là các tỉ số lượng giác đã được học ở lớp 9?
Chứng minh rằng với mọi tam giác ABC, ta có a = 2RsinA, b = 2RsinB, c = 2RsinC, trong đó R là bán kính đường tròn ngoại tiếp tam giác.
Cho 2 điểm phần biệt A, B. Xác định điểm M sao cho 2MA-3MB=0. Chứng minh rằng với mọi điểm Q ta luôn có 2QA-3QB=-QM ( vecto)
Chứng minh rằng với mọi α, ta luôn có
cos(α + π/2) = -sinα
Chứng minh rằng với mọi α, ta luôn có sin(α + π/2) = cosα