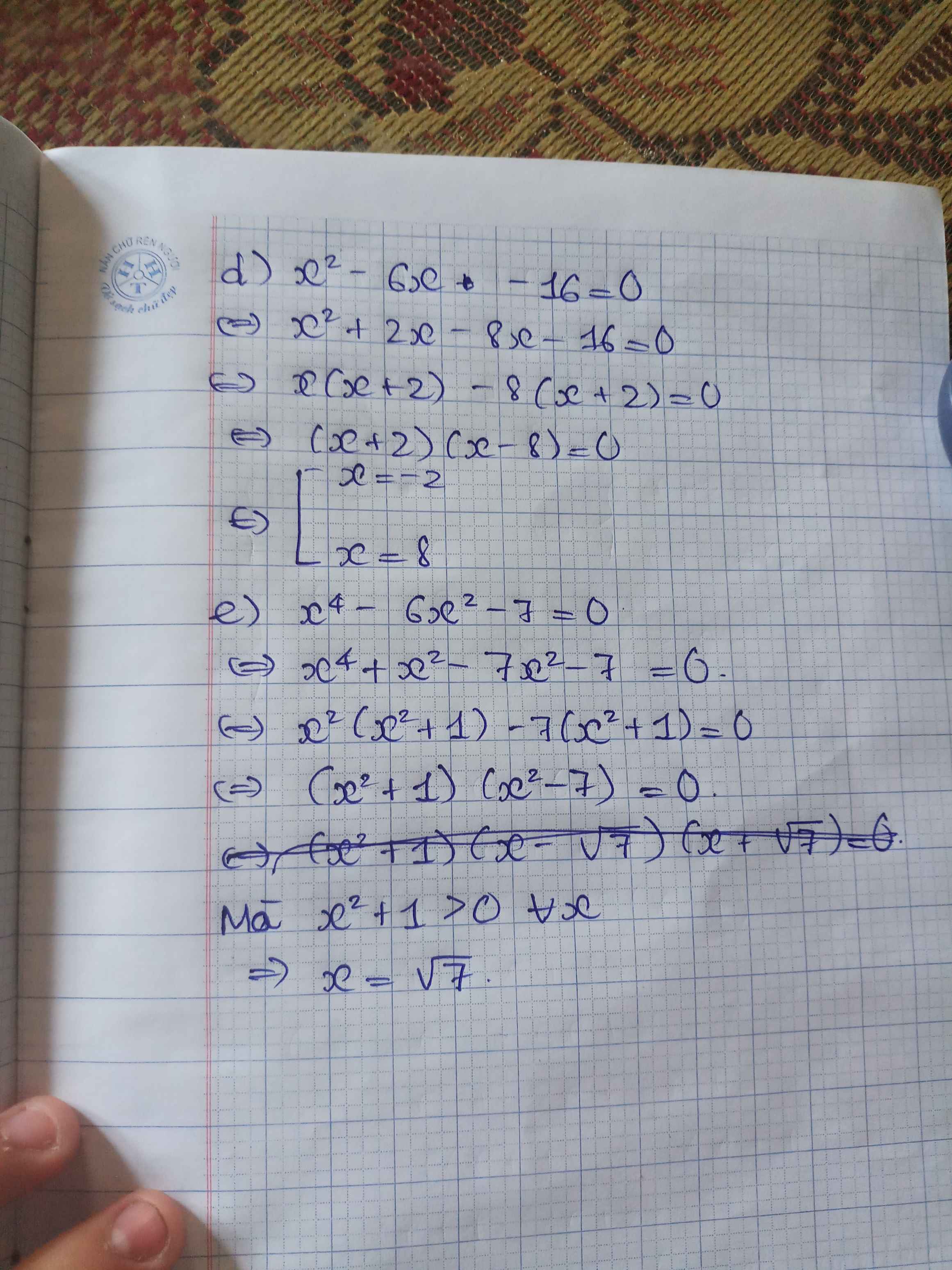Tìm x: (x2 + 7) . (x2 - 16) < 0
LP
Những câu hỏi liên quan
Tìm x:
a) 36x3-4x=0
b) 3x(x-2)-2+x=0
c) (x3-x2)-4x2+8x-4=0
d) x2-6x-16=0
e) x4-6x2-7=0
Tìm x biết:
a/ 5x( x- 3) = x – 3 b/ x3 - x = 0 c/ x2 – 7x + 6 = 0
d/ x2 – 4 + ( x – 2)2 = 0 e/ x2 – 16 –( x +4) = 0 f/ x2 + x – 2 = 0
a: \(\Leftrightarrow\left(x-3\right)\left(5x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=\dfrac{1}{5}\end{matrix}\right.\)
b: \(\Leftrightarrow x\left(x-1\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\\x=-1\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Tìm x:
a) 36x3-4x=0
b) 3x(x-2)-2+x=0
c) (x3-x2)-4x2+8x-4=0
d) x2-6x-16=0
e) x4-6x2-7=0
(Mình cần gấp ạ)
a) Ta có: \(36x^3-4x=0\)
\(\Leftrightarrow4x\left(9x^2-1\right)=0\)
\(\Leftrightarrow x\left(3x-1\right)\left(3x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{1}{3}\\x=\dfrac{-1}{3}\end{matrix}\right.\)
b) Ta có: \(3x\left(x-2\right)+x-2=0\)
\(\Leftrightarrow\left(x-2\right)\left(3x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=\dfrac{-1}{3}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
d) Ta có: \(x^2-6x-16=0\)
\(\Leftrightarrow\left(x-8\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=8\\x=-2\end{matrix}\right.\)
e) Ta có: \(x^4-6x^2-7=0\)
\(\Leftrightarrow\left(x^2-7\right)\left(x^2+1\right)=0\)
\(\Leftrightarrow x\in\left\{\sqrt{7};-\sqrt{7}\right\}\)
Đúng 0
Bình luận (0)
Tìm số nguyên x sao cho :
x2 = 0 ; x2 =16
\(x^2=0\)
\(\Rightarrow x^2=0^2\)
\(\Rightarrow x=0\)
-----------
\(x^2=16\)
\(\Rightarrow x^2=\left(\pm4\right)^2\)
\(\Rightarrow\left[{}\begin{matrix}x^2=\left(-4\right)^2\\x^2=4^2\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-4\\x=4\end{matrix}\right.\)
Đúng 3
Bình luận (0)
\(x^2=0\)
\(\Rightarrow x=0\left(tm\right)\)
Vậy: \(x=0.\)
\(---\)
\(x^2=16\)
\(\Rightarrow x^2=\left(\pm4\right)^2\)
\(\Rightarrow\left[{}\begin{matrix}x=4\left(tm\right)\\x=-4\left(tm\right)\end{matrix}\right.\)
Vậy: \(x\in\left\{4;-4\right\}.\)
Đúng 2
Bình luận (0)
Giải các phương trình:a)
3
x
−
3
4
−
2
−
4
x
0
;b)
x
2
−
4
x
+
7...
Đọc tiếp
Giải các phương trình:
a) 3 x − 3 4 − 2 − 4 x = 0 ;
b) x 2 − 4 x + 7 − 12 x + 7 = 0 ;
c) 4 − 4 + x + x x 2 − 16 = 0 ;
d) x 2 + 6 x − 7 = 0 .
Tìm các số nguyên x, biết:
a, (22 + 5)(x2 + 25) = 0
b, (x2 + 7)(x2 - 49) < 0
c, (x2 - 7)(x2 - 49) < 0
d, (x2 - 36)(x2 - 81) ≤ 0
Tìm x:
a) x2+9x=0
b) (x+4)2-16=0
c) x3-16x=0
d) x2-10x+25=0
\(a,\Leftrightarrow x\left(x+9\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-9\end{matrix}\right.\\ b,\Leftrightarrow\left(x+4-4\right)\left(x+4+4\right)=0\\ \Leftrightarrow x\left(x+8\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-8\end{matrix}\right.\\ c,\Leftrightarrow x\left(x-4\right)\left(x+4\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\\x=-4\end{matrix}\right.\\ d,\Leftrightarrow\left(x-5\right)^2=0\Leftrightarrow x=5\)
Đúng 2
Bình luận (0)
a) \(\Leftrightarrow x\left(x+9\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=-9\end{matrix}\right.\)
b) \(\Leftrightarrow x\left(x+8\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=-8\end{matrix}\right.\)
c) \(\Leftrightarrow x\left(x-4\right)\left(x+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\\x=-4\end{matrix}\right.\)
d) \(\Leftrightarrow\left(x-5\right)^2=0\\ \Leftrightarrow x=5\)
Đúng 0
Bình luận (1)
Tìm x ∈ Z, biết :
( x2 + 7 )( x2 - 7 ) < 0
(x² + 7)(x² - 7) < 0
⇒ x² - 7 < 0
⇒ x² < 7
⇒ -√7 < x < √7
Mà x ∈ Z
⇒ x ∈ {-2; -1; 0; 1; 2}
Đúng 2
Bình luận (0)
Tìm x ∈ Z ,biết :
( x2 + 7 )( x2 - 7 ) < 0
\(\left(x^2+7\right)\left(x^2-7\right)< 0\)
mà \(x^2+7>=7>0\forall x\)
nên \(x^2-7< 0\)
=>\(x^2< 7\)
=>\(-\sqrt{7}< x< \sqrt{7}\)
mà x nguyên
nên \(x\in\left\{-2;-1;0;1;2\right\}\)
Đúng 1
Bình luận (0)
h*) (x + 3)(1 – x) > 0
i*) (x2 – 1)(x2 – 4) < 0
k*) (x2 – 20)(x2 – 30) < 0
Bài 4: Tìm các số nguyên x sao cho
a) –3 ⋮ (x – 2)
b) (3x + 7) ⋮ (x – 2)
c*) (x2 + 7x + 2) ⋮ (x + 7)
a, \(\Rightarrow x-2\inƯ\left(-3\right)=\left\{\pm1;\pm3\right\}\)
| x-2 | 1 | -1 | 3 | -3 |
| x | 3 | 1 | 5 | -1 |
b, \(3\left(x-2\right)+13⋮x-2\Rightarrow x-2\inƯ\left(13\right)=\left\{\pm1;\pm13\right\}\)
| x-2 | 1 | -1 | 13 | -13 |
| x | 3 | 1 | 15 | -11 |
c, \(x\left(x+7\right)+2⋮x+7\Rightarrow x+7\inƯ\left(2\right)=\left\{\pm1;\pm2\right\}\)
| x+7 | 1 | -1 | 2 | -2 |
| x | -6 | -8 | -5 | -9 |
Đúng 0
Bình luận (0)