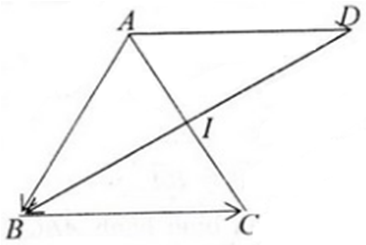
Cho tam giác đều ABC cạnh bằng a. Tính độ dài của các vectơ 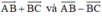
PB
Những câu hỏi liên quan
Cho tam giác đều ABC có cạnh bằng a. Tính độ dài của các vectơ \(\overrightarrow {AB} - \overrightarrow {AC} ,\;\overrightarrow {AB} + \overrightarrow {AC} .\)
Tham khảo:
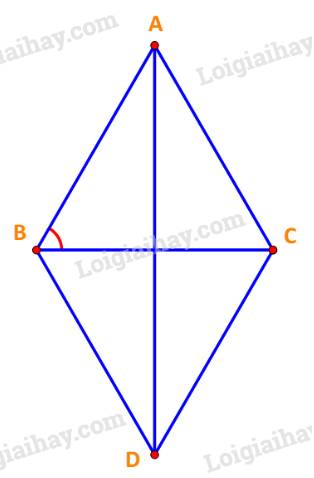
\(\overrightarrow {AB} - \overrightarrow {AC} = \overrightarrow {CB} \Rightarrow \left| {\overrightarrow {AB} - \overrightarrow {AC} } \right| = \left| {\overrightarrow {CB} } \right| = CB = a.\)
Dựng hình bình hành ABDC tâm O như hình vẽ.
Ta có:
\(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {AD} \)
\( \Rightarrow \left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AD} } \right| = AD\)
Vì tứ giác ABDC là hình bình hành, lại có \(AB = AC = BD = CD = a\) nên ABDC là hình thoi.
\( \Rightarrow AD = 2AO = 2.AB.\sin B = 2a.\frac{{\sqrt 3 }}{2} = a\sqrt 3 .\)
Vậy \(\left| {\overrightarrow {AB} - \overrightarrow {AC} } \right| = a\) và \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = a\sqrt 3 \).
Đúng 0
Bình luận (0)
Cho tam giác đều ABC với cạnh có độ dài bằng a. Hãy chỉ ra các vectơ có độ dài bằng a và có điểm đầu, điểm cuối là các đỉnh của tam giác ABC.
Các vectơ có độ dài bằng a và có điểm đầu, điểm cuối là các đỉnh của tam giác ABC là:
\(\overrightarrow {AB} ;\;\overrightarrow {BA} ;\;\overrightarrow {AC} ;\;\overrightarrow {CA} ;\;\overrightarrow {BC} ;\;\overrightarrow {CB} \)
Chú ý khi giải:
Vectơ \(\overrightarrow {AB} \) khác vectơ \(\overrightarrow {BA} \) (khác nhau điểm đầu và điểm cuối).
Đúng 0
Bình luận (0)
Cho tam giác ABC đều cạnh a. Tính độ dài vectơ 2AB + 3AC
Cho tam giác đều ABC cạnh a, đường cao AH. Hỏi a√3 là độ dài của vectơ nào trong số các vectơ sau đây? A.
A
H
→
B.
A
B
→
-
A
C
→
C.
A
B
→
+
...
Đọc tiếp
Cho tam giác đều ABC cạnh a, đường cao AH. Hỏi a√3 là độ dài của vectơ nào trong số các vectơ sau đây?
A. A H →
B. A B → - A C →
C. A B → + A C →
D. A B → + A C → - A H →
Dựng điểm D sao cho H là trung điểm AD.
Ta có; H là trung điểm của mỗi đường AD ; BC. Do đó, tứ giác ACDB là hình bình hành.
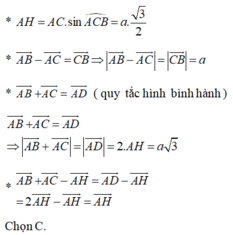
Đúng 0
Bình luận (0)
Cho tam giác đều ABC cạnh bằng a và điểm M di động trên đường thẳng BC. Tính độ dài nhỏ nhất của vectơ u= MA +MB+ MC.
Gọi G là trọng tâm tam giác
\(\left|\overrightarrow{u}\right|=\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|=\left|\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{MG}+\overrightarrow{GB}+\overrightarrow{MG}+\overrightarrow{GC}\right|\)
\(=\left|3\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\right|=\left|3\overrightarrow{MG}\right|=3MG\)
\(\Rightarrow\left|\overrightarrow{u}\right|_{min}\) khi \(MG_{min}\)
\(\Rightarrow M\) là chân đường vuông góc hạ từ G xuống BC hay M là trung điểm BC
\(\Rightarrow\left|\overrightarrow{u}\right|_{min}=3MG=AM=\dfrac{a\sqrt{3}}{2}\)
Đúng 0
Bình luận (0)
Cho tam giác đều ABC cạnh có độ dài là a. Tính độ dài vectơ \(\overrightarrow {AB} + \overrightarrow {AC}\)
Dựng hình bình hành ABDC.
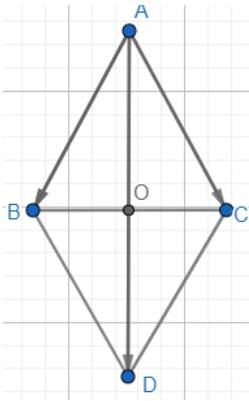
Áp dụng quy tắc hình bình hành vào ABDC ta có:
\(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AD} \Rightarrow \left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AD} } \right| = AD\)
Gọi O là giao điểm của AD và BC, ta có:
\(AO = \sqrt {A{B^2} - B{O^2}} = \sqrt {A{B^2} - {{\left( {\frac{1}{2}BC} \right)}^2}} = \sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 3 }}{2}\)
\(AD = 2AO = a\sqrt 3 \Rightarrow \left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = a\sqrt 3 \)
Vậy độ dài vectơ \(\overrightarrow {AB} + \overrightarrow {AC} \) là \(a\sqrt 3 \)
Đúng 0
Bình luận (0)
Cho tam giác đều ABC cạnh bằng a. Tính độ dài của các vectơ \(\overrightarrow{AB}+\overrightarrow{BC}\) và \(\overrightarrow{AB}-\overrightarrow{BC}\) ?
Cho tam giác ABC đều cạnh a, trực tâm H. Tính độ dài của các vectơ \(\overrightarrow{HA},\overrightarrow{HB},\overrightarrow{HC}\)
\(\left|\overrightarrow{HA}\right|=\left|\overrightarrow{HB}\right|=\left|\overrightarrow{HC}\right|=\dfrac{2}{3}\cdot\dfrac{a\sqrt{2}}{3}=\dfrac{2a\sqrt{2}}{9}\)
Đúng 0
Bình luận (0)
CHo tam giác ABC đều có cạnh là 6. Gọi M, N, P lần lượt là ttrung điểm của AB, AC, BC.
â. kể tên các vectơ bằng vectơ MN
b. tính độ dài vecto MNnhaan độ dài vecto AP
c. hạ PH vuông góc với AC tại H. tính độ dài vecto PH