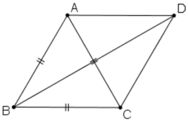
Ta có:
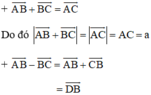
(Quy tắc hình bình hành)
(Trong đó D là đỉnh còn lại của hình bình hành ABCD)
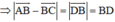
+ Tính BD:
Hình bình hành ABCD có AB = BC = a nên ABCD là hình thoi.
⇒ AC ⊥ BD tại O là trung điểm của AC và BD.
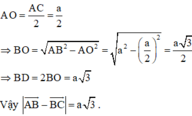

Ta có:
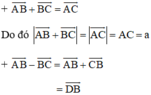
(Quy tắc hình bình hành)
(Trong đó D là đỉnh còn lại của hình bình hành ABCD)
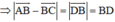
+ Tính BD:
Hình bình hành ABCD có AB = BC = a nên ABCD là hình thoi.
⇒ AC ⊥ BD tại O là trung điểm của AC và BD.
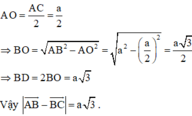
Cho tam giác đều ABC cạnh a, đường cao AH. Hỏi a√3 là độ dài của vectơ nào trong số các vectơ sau đây?
A. A H →
B. A B → - A C →
C. A B → + A C →
D. A B → + A C → - A H →
Cho tam giác đều ABC cạnh bằng a và điểm M di động trên đường thẳng BC. Tính độ dài nhỏ nhất của vectơ u= MA +MB+ MC.
Cho tam giác ABC đều cạnh 2a. Khi đó độ dài vectơ A B → + A C → bằng
A. 2a
B. 2 a 3
C. 4a
D. a 3
Cho tam giác ABC đều, cạnh , trọng tâm G. Độ dài vectơ \(\overline{AB} \) - \(\overline{GC} \) là
Cho tam giác đều ABC có cạnh bằng 6cm. Một điểm M nằm trên cạnh BC sao cho BM = 2cm.
a, Tính độ dài của đoạn thẳng AM và tính côsin của góc BAM ;
b, Tính bán kính đường tròn ngoại tiếp tam giác ABM;
c, Tính độ dài đường trung tuyến vẽ từ đỉnh C của tam giác ACM;
d, Tính diện tích tam giác ABM.
Gọi G là trọng tâm tam giác vuông ABC với cạnh huyền BC = 12. Tính độ dài của vectơ v → = G B → + G C → .
![]()
![]()
![]()
![]()
Cho tam giác ABC đều cạnh a có trọng tâm G và điểm I thỏa vecto IA -2 vectơ IB +4 vectơ IC= vectơ 0 tính biểu thức P= vectơ IA.(vtAB+vtAC) theo a
Câu 6: Cho tàm giác ABC có A(1; - 1) ;B(2; 0) ;C(3; 5) a) Tìm tọa độ các vecto AB ,AC ,BC b) Tính độ dài các cạnh của tam giác ABC. Từ đó tính chu vi tam giác. c) Tìm tọa độ trung điểm các cạnh và tìm tọa độ trọng tâm của tam giác ABC. d) Tìm tọa độ điểm D để tứ giác ABCD là hnh bình hành e) Tọa độ chân đường cao xuất phát từ A của tam giác. Đ) Tính góc A?
Cho tam giác ABC vuông tại A có A B = 5 , A C = 2 5
Độ dài vectơ A C → - A B → bằng:
A. 5
B. 15
C. 5
D. 2