Nghiệm (x; y) của hệ phương trình 2 x + 2 y + 1 2 x + y = 3 4 x + 2 y + 3 2 x + y = 1 là:
A. 13 60 ; − 7 30
B. − 13 60 ; − 7 30
C. − 13 60 ; 7 30
D. 13 60 ; 7 30
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Cho f(x)=x^2 -2(m-2)x+m+10. Định m để:
a. Phương trình f(x)=0 có một nghiệm x= 1 và tính nghiệm kia
b. Phương trình f(x)=0 có nghiệm kép. Tính nghiệm kép đó.
c. Tìm m để phương trình f(x)=0 có 2 nghiệm âm phân biệt.
d. Tìm m để f(x)<0 có nghiệm đúng với mọi xϵR
a.
\(f\left(x\right)=0\) có nghiệm \(x=1\Rightarrow f\left(1\right)=0\)
\(\Rightarrow1-2\left(m-2\right)+m+10=0\)
\(\Rightarrow m=15\)
Khi đó nghiệm còn lại là: \(x_2=\dfrac{m+10}{x_1}=\dfrac{25}{1}=25\)
b.
Pt có nghiệm kép khi: \(\Delta'=\left(m-2\right)^2-\left(m+10\right)=0\)
\(\Rightarrow m^2-5m-6=0\Rightarrow\left[{}\begin{matrix}m=-1\\m=6\end{matrix}\right.\)
Với \(m=-1\) nghiệm kép là: \(x=-\dfrac{b}{2a}=m-2=-3\)
Với \(m=6\) nghiệm kép là: \(x=-\dfrac{b}{2a}=m-2=4\)
c.
Pt có 2 nghiệm âm pb khi:
\(\left\{{}\begin{matrix}\Delta'=m^2-5m-6>0\\x_1+x_2=2\left(m-2\right)< 0\\x_1x_2=m+10>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m< -1\\m>6\end{matrix}\right.\\m< 2\\m>-10\end{matrix}\right.\) \(\Rightarrow-10< m< -1\)
d.
\(f\left(x\right)< 0;\forall x\in R\Rightarrow\left\{{}\begin{matrix}a=1< 0\left(\text{vô lý}\right)\\\Delta'=m^2-5m-6< 0\end{matrix}\right.\)
Không tồn tại m thỏa mãn
Cho phương trình : 2|x|^3 - 9x^2 + 12 |x| + m = 0 (1)
Tìm m để (1) có : 6 nghiệm , 5 nghiệm , 4 nghiệm , 3 nghiệm , 2 nghiệm , 1 nghiệm , 0 nghiệm
Hướng dẫn:
Bạn khảo sát hàm \(y=f\left(x\right)=2x^3-9x^2+12x\) với \(x\ge0\)
Sau đó lấy đối xứng đồ thị (hoặc BBT) qua trục Oy sẽ được hàm \(y=f\left(\left|x\right|\right)=2\left|x\right|^3-9x^2+12\left|x\right|\)
Nhìn vào đồ thị (hoặc BBT), bạn biện luận số giao điểm của \(y=-m\) và \(y=f\left(\left|x\right|\right)\) dễ dàng
Biết phương trình x − 2 + x + a x − 1 = a có nghiệm duy nhất và nghiệm đó là nghiệm nguyên. Vậy nghiệm đó là:
A. -2
B. -1
C. 2
D. 0
Điều kiện: x ≠ 1
Phương trình (1) thành:
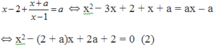
Phương trình (1) có nghiệm duy nhất.
⇔ Phương trình (2) có nghiệm duy nhất khác 1 hoặc phương trình (2) có 2 nghiệm phân biệt có một nghiệm bằng 1
⇔ Δ = 0 x = − b 2 a ≠ 1 Δ > 0 f ( 1 ) = 0 ⇔ a 2 − 4 a − 4 = 0 a + 2 2 ≠ 1 a 2 − 4 a − 4 > 0 1 − 2 − a + 2 a + 2 = 0
⇔ a 2 − 4 a − 4 = 0 a + 2 ≠ 2 a 2 − 4 a − 4 > 0 a + 1 = 0 ⇔ a = 2 + 2 2 a = 2 − 2 2 a = − 1
Với a = 2 + 2 2 phương trình có nghiệm là x = 2 + 2
Với a = 2 − 2 2 phương trình có nghiệm là x = 2 − 2
Với a = -1 phương trình có nghiệm là: x = 0 ( n ) x = 1 ( l )
Đáp án cần chọn là: D
Phương trình x2=-4 có nghiệm là:
A. Một nghiệm x=2 B. Một nghiệm x=-2 C. Có hai nghiệm:x=-2;x=2 D. Vô nghiệm
Phương trình x2 = -4 có nghiệm là:
A. Một nghiệm x=2
B. Một nghiệm x=-2
C. Có hai nghiệm:x=-2;x=2
D. Vô nghiệm
cho đa thức : h(x) = x^4 + 1/2x^2 + 2012 . chứng tỏ h(x) vô nghiệm
CTR đa thứa : 3x^2010 + x^1002+ 1 vô nghiệm
CTR đa Thức : M(x)= x^2 + 2x + 2 vô nghiệm
CTR đa thức : M(x) = x^2 + 2x + 1 chỉ có 1 nghiệm duy nhất tìm nghiệm duy nhất đó
CMR đa thức M(x) = x^2 - x + 5 không có nghiệm nguyên
tìm m để phương trình
a, x2 - 5x + 6 = 0 nhận x=m là nghiệm, tìm nghiệm còn lại
b, x - 5x +4 = 0 nhận x = m + 1 làm nghiệm, tìm nghiệm còn lại
c, 2018x + x - 2019 = 0 nhận x = 2m - 1 làm nghiệm, tìm nghiệm còn lại
cái x đầu ở câu b và c là x2 nha
quên không chỉnh :))
1. Tìm m để pt \(\left(x^2+2x\right)^2-\left(x^2+2x\right)-m=0\)
a .có 4 nghiệm pb
b. vô ng
c. có nghiệm duy nhất
d. có nghiệm
e. có nghiệm kép
2. Biết pt: \(x+\sqrt{2x+11}=0\) có nghiệm \(x=a+b\sqrt{3}\). Tính ab
HELP ME
Bài 2.
ĐK: $x\geq \frac{-11}{2}$
$x+\sqrt{2x+11}=0\Leftrightarrow x=-\sqrt{2x+11}$
\(\Rightarrow \left\{\begin{matrix} x\leq 0\\ x^2=2x+11\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\leq 0\\ x^2-2x-11=0(*)\end{matrix}\right.\)
\(\Delta'(*)=12\)
\(\Rightarrow x=1\pm \sqrt{12}=1\pm 2\sqrt{3}\). Với điều kiện của $x$ suy ra $x=1-2\sqrt{3}$
$\Rightarrow a=1; b=-2\Rightarrow ab=-2$
Bài 1.
Đặt $x^2+2x=t$ thì PT ban đầu trở thành:
$t^2-t-m=0(1)$
Để PT ban đầu có 4 nghiệm phân biệt thì:
Trước tiên PT(1) cần có 2 nghiệm phân biệt. Điều này xảy ra khi $\Delta (1)=1+4m>0\Leftrightarrow m> \frac{-1}{4}(*)$
Với mỗi nghiệm $t$ tìm được, thì PT $x^2+2x-t=0(2)$ cần có 2 nghiệm $x$ phân biệt.
Điều này xảy ra khi $\Delta '(2)=1+t>0\Leftrightarrow t>-1$
Vậy ta cần tìm điều kiện của $m$ để (1) có hai nghiệm $t$ phân biệt đều lớn hơn $-1$
Điều này xảy ra khi \(\left\{\begin{matrix} (t_1+1)(t_2+1)>0\\ t_1+t_2+2>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} t_1t_2+t_1+t_2+1>0\\ t_1+t_2+2>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} -m+1+1>0\\ 1+2>0\end{matrix}\right.\Leftrightarrow m< 2(**)\)
Từ $(*); (**)\Rightarrow \frac{-1}{4}< m< 2$
b)
Để pt ban đầu vô nghiệm thì PT(1) vô nghiệm hoặc có 2 nghiệm $t$ đều nhỏ hơn $-1$
PT(1) vô nghiệm khi mà $\Delta (1)=4m+1<0\Leftrightarrow m< \frac{-1}{4}$
Nếu PT(1) có nghiệm thì $t_1+t_2=1>-2$ nên 2 nghiệm $t$ không thể cùng nhỏ hơn $-1$
Vậy PT ban đầu vô nghiệm thì $m< \frac{-1}{4}$
c) Để PT ban đầu có nghiệm duy nhất thì:
\(\left\{\begin{matrix} \Delta (1)=1+4m=0\\ \Delta' (2)=1+t=0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m=-\frac{1}{4}\\ t=-1\end{matrix}\right.\).Mà với $m=-\frac{1}{4}$ thì $t=\frac{1}{2}$ nên hệ trên vô lý. Tức là không tồn tại $m$ để PT ban đầu có nghiệm duy nhất.
d)
Ngược lại phần b, $m\geq \frac{-1}{4}$
e)
Để PT ban đầu có nghiệm kép thì PT $(2)$ có nghiệm kép. Điều này xảy ra khi $\Delta' (2)=1+t=0\Leftrightarrow t=-1$
$t=-1\Leftrightarrow m=(-1)^2-(-1)=2$
Tìm m để phương trình x(x+1)(x+2)(x+3) + 4 - 3m =0 a) VN b) có 2 nghiệm c) có 3 nghiệm d) có 4 nghiệm e) có nghiệm duy nhất
Mình sẽ chụp ₫áp án cho bạn qua Zalo Lạc Thiên Y. Cho mình Zalo của bạn nhé
Cho phương trình 2x2 - (4m + 3)x + 2m2 - 1 = 0 . Tìm các giá trị của m để phương trình:
a) Có hai nghiệm phân biệt?
b) Có nghiệm kép; tìm nghiệm kép đó?
c) Vô nghiệm?
d) có nghiệm x = -1? Tìm nghiệm còn lại?
a: Δ=(4m+3)^2-4*2*(2m^2-1)
=16m^2+24m+9-16m^2+8
=24m+17
Để phương trình có hai nghiệm phân biệt thì 24m+17>0
=>m>-17/24
b: Để phương trìh có nghiệm kép thì 24m+17=0
=>m=-17/24
c: Để phương trình vô nghiệm thì 24m+17<0
=>m<-17/24
Khẳng định nào sau đây là đúng?
(A) Đa thức 5x5 không có nghiệm;
(B) Đa thức x2 - 2 không có nghiệm;
(C) Đa thức x2 + 2 có nghiệm x = -1;
(D) Đa thức x có nghiệm x = 0
Đáp án đúng là (D) Đa thức x có nghiệm x = 0.