cho hình chóp SABCD đáy là hình vuông cạnh A, SA\(\perp\) với đáy, SA=a\(\sqrt{2}\) , mp (P) đi qua A vuông góc với SC tại M và cắt SB, SD tại N,P. c/m
a.tứ giác ANMP là hình thoi
b.diện tích ANMP=\(\dfrac{\sqrt{2}a^2}{3}\)
cho hình chóp SABCD đáy là hình vuông cạnh A, SA\(\perp\) với đáy, SA=a\(\sqrt{2}\) , mp (P) đi qua A vuông góc với SC tại M và cắt SB, SD tại N,P. c/m
a.tứ giác ANMP là hình thoi
b.diện tích ANMP=\(\dfrac{\sqrt{2}a^2}{3}\)
Ba khẩu súng cùng bắn vào 1 mục tiêu độc lập nhau với sác xuất bắn trúng của mỗi khẩu là 0,8 ; 0,6;0,7 .gọi X là số viên đạn bắn trúng mục tiêu . Hãy lập bản phân phối xác xuất của X
gọi m, M tương ứng với giá trị lớn nhất và nhỏ nhất của hàm số y= x^3 -3x^2 +kx +4 trên đoạn [-1;3] biết M+m=3
You can learn the difficult concept to understand from Solvemate. This is a education service for using technology to adapt in order to create mathematical problems based on the learning needs of students.
Math mate in your pocket. https://intro.solve-mate.com/
\(\left|2z-3+i\right|=\left|z-5+2i\right|\)
Yêu cầu đề bài là gì thế bạn?
Cho \(\left\{{}\begin{matrix}x;y;z>0\\x^2+y^2+z^2=x\left(y+z\right)+10yz\end{matrix}\right.\)
Tìm max của \(P=8xyz-\dfrac{3x^3}{y^2+z^2}\)
Biểu thức này chỉ có min, không có max
\(x^2+y^2+z^2=xy+xz+10yz\)
\(\Leftrightarrow\dfrac{3x^2}{4}+\left(\dfrac{x}{2}-y-z\right)^2=12yz\)
\(\Rightarrow12yz\ge\dfrac{3}{4}x^2\Rightarrow yz\ge\dfrac{x^2}{16}\)
\(\Rightarrow P\ge\dfrac{x^3}{2}-\dfrac{3x^3}{2yz}\ge\dfrac{x^3}{2}-\dfrac{3x^3}{\dfrac{x^2}{8}}=\dfrac{x^3}{2}-24x\)
Xét hàm \(f\left(x\right)=\dfrac{x^3}{2}-24x\) với \(x>0\Rightarrow f'\left(x\right)=\dfrac{3}{2}x^2-24=0\Rightarrow x=4\)
Từ BBT ta thấy \(\min\limits_{x>0}f\left(x\right)=f\left(4\right)=-64\)
\(\Rightarrow P_{min}=-64\) khi \(\left(x;y;z\right)=\left(4;1;1\right)\)
toán rời rạc ạ. giúp mình với
tui nghĩ câu 1 như này ;-; thử lần lượt các trường hợp là được. Mấy câu dưới chắc cx z ~~

Lướt lại bài hồi trước giải và giờ đã có kthuc để giải
a/
b/
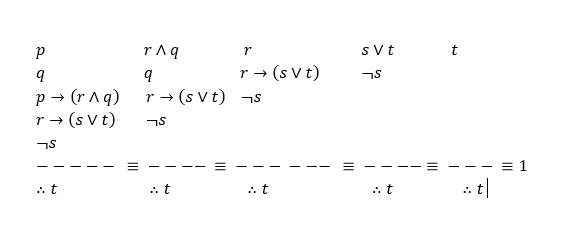
c/
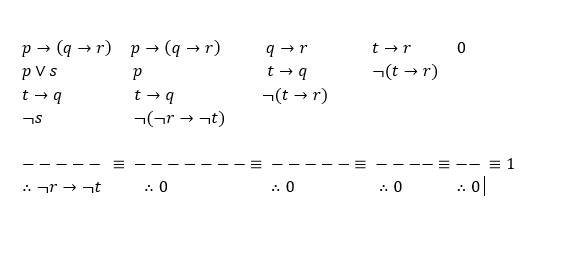
d/
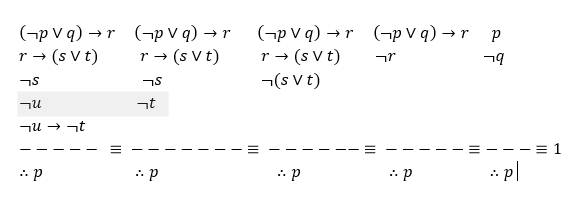
\(y=x^4-1\) có phải hàm bậc 4 trùng phương?
Tiệm cận ngang của đồ thị hàm số y = 3x +1/x-1 là:
\(\lim\limits_{x\rightarrow\infty}\dfrac{3x+1}{x-1}=3\Rightarrow y=3\) là TCN của đồ thị hàm số
Cho hình chóp S.abcd có SA vuông góc với mặt phẳng (ABCD), đáy ABCD là hình chữ nhật. SA =4a,AB=4a,AD=3a. Tính thể tích khối chóp
Mong mn giải giúp e nhé ♡
\(S_{ABCD}=AB.AD=4a.3a=12a^2\)
SA=4a
Thể tích khối chóp là :
\(V=\dfrac{1}{3}.S_{ABCD}.SA=\dfrac{1}{3}.12a.4a=16a^3\)
y=−x4+2mx2–2m+1y=−x4+2mx2–2m+1 ( mm là tham số) có đồ thị (Cm) a) khảo sát sự biến thiên và vẽ đths với m=1