* Xét tứ giác ABCD, ta có:

MA = MC (gt)

MB = MD (định nghĩa đối xứng tâm)

Suy ra: Tứ giác ABCD là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường)

⇒ AD // BC và AD = BC (1)

* Xét tứ giác ACBE, ta có:

AN = NB (gt)

NC = NE (định nghĩa đối xứng tâm)

Suy ra: Tứ giác ACBE là hình bình hành (vì có 2 đường chéo cắt nhau tại trung điểm của mỗi đường) ⇒ AE // BC và AE = BC (2)

Từ (1) và (2) suy ra: A, D, E thẳng hàng và AD = AE

Nên A là trung điểm của DE hay điểm D đối xứng với điểm E qua điểm A.

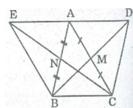
* Xét tứ giác ABCD, ta có:

MA = MC (gt)

MB = MD (định nghĩa đối xứng tâm)

Suy ra: Tứ giác ABCD là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường)

⇒ AD // BC và AD = BC (1)

* Xét tứ giác ACBE, ta có:

AN = NB (gt)

NC = NE (định nghĩa đối xứng tâm)

Suy ra: Tứ giác ACBE là hình bình hành (vì có 2 đường chéo cắt nhau tại trung điểm của mỗi đường) ⇒ AE // BC và AE = BC (2)

Từ (1) và (2) suy ra: A, D, E thẳng hàng và AD = AE

Nên A là trung điểm của DE hay điểm D đối xứng với điểm E qua điểm A.

xét tam giác ADE có:

AB=DB( gt)

AC=EC (gt)

=> BC//DE ( t/c đường trung bình)

ta có: BC//DE (CMT)

AM vuông góc với BC

AM=IM

=> góc AID= góc AIE

Xét tam giác AEI và tam giác ADIcó:

góc DAI= góc EAI

AI chung 

góc AID= góc AIE (CMT)

=> tam giác  AEI = tam giác ADI (g.c.g)

=> DI=EI(2 cạnh tương ứng)

Xét tứ giác ABCD có 

AM=CM; BM=DM => ABCD là hình bình hành (tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường là hbh)

=> AD//=BC

Xét ứ giác ACBE có

AN=BN; CN=EN => ACBE  là hình bình hành (tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường là hbh)

=> AE//=BC

=> AD=AE =BC

=> AE trùng AD hay A; D; E thẳng hàng (Qua 1 điểm ngoài đường thẳng chỉ dựng được duy nhất 1 đường thẳng // với đường thẳng đã cho)

=> D đối xứng với E qua A

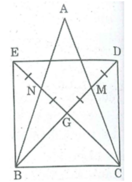
* Tam giác ABC có hai đường trung tuyến BM và CN cắt nhau tại G

Suy ra: G là trọng tâm của ∆ ABC .

⇒ GB = 2GM (tính chất đường trung tuyến)

GC = 2GN (tính chất đường trung tuyến)

Điểm D đối xứng với điểm G qua điểm M

⇒ MG = MD hay GD = 2GM

Suy ra: GB = GD (l)

Điểm E đối xứng với điểm G qua điểm N

⇒ NG = NE hay GE = 2GN

Suy ra: GC = GE (2)

Từ (1) và (2) suy ra tứ giác BCDE là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường)

Xét  ∆ BCM và  ∆ CBN, có: BC cạnh chung

∠ (BCM) =  ∠ (CBN) (tính chất tam giác cân)

CM = BN (vì AB = AC)

Suy ra:  ∆ BCM = ∆ CBN (c.g.c)

⇒  ∠ (MBC) =  ∠ (NCB) ⇒  ∆ GBC cân tại G ⇒ GB = GC ⇒ BD = CE

Hình bình hành BCDE có hai đường chéo bằng nhau nên nó là hình chữ nhật.

a: Xét tứ giác ABCD có

M là trung điểm chung của AC và BD

nên ABCD là hình bình hành

b: Xét tứ giác AEBC có

N là trung điểm chung của AB và EC

nên AEBC là hình bình hành

=>AE//BC và AE=BC

=>AD//AE và AD=AE
=>A là trung điểm của DE

Xét tứ giác AEBC có 

N là trung điểm của đường chéo AB

N là trung điểm của đường chéo CE

Do đó: AEBC là hình bình hành

Suy ra: AE//BC và AE=BC(1)

Xét tứ giác ADCB có 

M là trung điểm của đường chéo AC

M là trung điểm của đường chéo BD

Do đó: ADCB là hình bình hành

Suy ra: AD//BC và AD=BC(2)

Từ (1) và (2) suy ra E,A,D thẳng hàng và AE=AD

hay E và D đối xứng nhau qua A