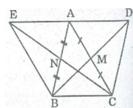
* Xét tứ giác ABCD, ta có:
MA = MC (gt)
MB = MD (định nghĩa đối xứng tâm)
Suy ra: Tứ giác ABCD là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường)
⇒ AD // BC và AD = BC (1)
* Xét tứ giác ACBE, ta có:
AN = NB (gt)
NC = NE (định nghĩa đối xứng tâm)
Suy ra: Tứ giác ACBE là hình bình hành (vì có 2 đường chéo cắt nhau tại trung điểm của mỗi đường) ⇒ AE // BC và AE = BC (2)
Từ (1) và (2) suy ra: A, D, E thẳng hàng và AD = AE
Nên A là trung điểm của DE hay điểm D đối xứng với điểm E qua điểm A.
xét tam giác ADE có:
AB=DB( gt)
AC=EC (gt)
=> BC//DE ( t/c đường trung bình)
ta có: BC//DE (CMT)
AM vuông góc với BC
AM=IM
=> góc AID= góc AIE
Xét tam giác AEI và tam giác ADIcó:
góc DAI= góc EAI
AI chung
góc AID= góc AIE (CMT)
=> tam giác AEI = tam giác ADI (g.c.g)
=> DI=EI(2 cạnh tương ứng)

