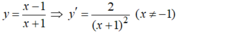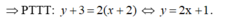\(y'=\dfrac{-1}{\left(x-1\right)^2}\)

Gọi tiếp tuyến qua điểm \(M\left(a;b\right)\) thuộc (C) có dạng:

\(y=\dfrac{-1}{\left(a-1\right)^2}\left(x-a\right)+\dfrac{2a-1}{a-1}\)

\(\Leftrightarrow x+\left(a-1\right)^2y-2a^2+2a-1=0\)

Áp dụng công thức khoảng cách:

\(\dfrac{\left|1+2\left(a-1\right)^2-2a^2+2a-1\right|}{\sqrt{1+\left(a-1\right)^4}}=\sqrt{2}\)

\(\Leftrightarrow\left|2a-2\right|=\sqrt{2}.\sqrt{1+\left(a-1\right)^4}\)

\(\Leftrightarrow2\left(a-1\right)^2=1+\left(a-1\right)^4\)

\(\Leftrightarrow\left[\left(a-1\right)^2-1\right]^2=0\Rightarrow a=...\)

b.

Vẫn từ công thức khoảng cách trên:

\(d=\dfrac{\left|2a-2\right|}{\sqrt{1+\left(a-1\right)^4}}=\dfrac{2\sqrt{\left(a-1\right)^2}}{\sqrt{1+\left(a-1\right)^4}}=\dfrac{2}{\sqrt{\dfrac{1}{\left(a-1\right)^2}+\left(a-1\right)^2}}\)

\(d\le\dfrac{2}{\sqrt{2\sqrt{\dfrac{\left(a-1\right)^2}{\left(a-1\right)^2}}}}=\sqrt{2}\)

Vậy \(d_{max}=\sqrt{2}\) khi tiếp tuyến trùng với các tiếp tuyến câu a

Ta có : \(y=\dfrac{x-1}{x+1}\Rightarrow y'=\dfrac{\left(x+1\right)-\left(x-1\right)}{\left(x+1\right)^2}=\dfrac{2}{\left(x+1\right)^2}\)

Giả sử d' là tiếp tuyến của đths đã cho . Do d' // d : y = \(\dfrac{x-2}{2}\)

\(\Rightarrow d'\) có HSG = 1/2 \(\Rightarrow\dfrac{2}{\left(x+1\right)^2}=\dfrac{1}{2}\Leftrightarrow4=\left(x+1\right)^2\)  \(\Leftrightarrow\left[{}\begin{matrix}x+1=2\\x+1=-2\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-3\end{matrix}\right.\) 

Với x = 1 . PTTT d' : \(y=\dfrac{1}{2}\left(x-1\right)+0=\dfrac{1}{2}x-\dfrac{1}{2}\)

Với x = -3 . PTTT d' : \(y=\dfrac{1}{2}\left(x+3\right)+2=\dfrac{1}{2}x+\dfrac{7}{2}\)

y'=(x-1)'(x+1)-(x-1)(x+1)'/(x+1)^2=(x+1-x+1)/(x+1)^2=2/(x+1)^2

(d1)//(d)

=>(d1): y=1/2x+b

=>y'=1/2

=>(x+1)^2=4

=>x=1 hoặc x=-3

Khi x=1 thì f(1)=0

y-f(1)=f'(1)(x-1)

=>y-0=1/2(x-1)=1/2x-1/2

Khi x=-3 thì f(-3)=(-4)/(-2)=2

y-f(-3)=f'(-3)(x+3)

=>y-2=1/2(x+3)

=>y=1/2x+3/2+2=1/2x+7/2

Với x = –2 ta có: y = –3 và y'(2) = 2.

Y=9x+7

https://drive.google.com/file/d/14Q-YI3szy-rePnIHWGD35RKCWiCXCT6k/view?usp=sharing

Đáp án là A

\(y'=\dfrac{13}{\left(x+3\right)^2}\) \(\Rightarrow\left\{{}\begin{matrix}y'\left(10\right)=\dfrac{1}{13}\\y\left(10\right)=3\end{matrix}\right.\)

Phương trình tiếp tuyến:

\(y=\dfrac{1}{13}\left(x-10\right)+3\Leftrightarrow y=\dfrac{1}{13}x+\dfrac{29}{13}\)

a.

\(y'=\dfrac{\left(sinx+cosx\right)'}{2\sqrt{sinx+cosx}}=\dfrac{cosx-sinx}{2\sqrt{sinx+cosx}}\)

b.

\(y'=\dfrac{-4}{\left(x-1\right)^2}\)

Tiếp tuyến vuông góc với \(y=\dfrac{1}{4}x+5\) nên có hệ số góc thỏa mãn \(k.\left(\dfrac{1}{4}\right)=-1\Rightarrow k=-4\)

\(\Rightarrow\dfrac{-4}{\left(x-1\right)^2}=-4\Rightarrow\left(x-1\right)^2=1\)

\(\Rightarrow\left[{}\begin{matrix}x=0\Rightarrow y=-3\\x=2\Rightarrow y=5\end{matrix}\right.\)

Có 2 tiếp tuyến thỏa mãn: \(\left[{}\begin{matrix}y=-4x-3\\y=-4\left(x-2\right)+5\end{matrix}\right.\)