Tìm các khoảng đồng biến, nghịch biến của các hàm số:
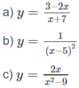
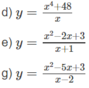
Tìm các khoảng đồng biến- nghịch biến của các hàm số sau


q.
\(y=x^4-4x^2+3\)
\(y'=4x^3-8x=0\Rightarrow\left[{}\begin{matrix}x=-\sqrt{2}\\x=\sqrt{2}\\x=0\end{matrix}\right.\)
BBT:
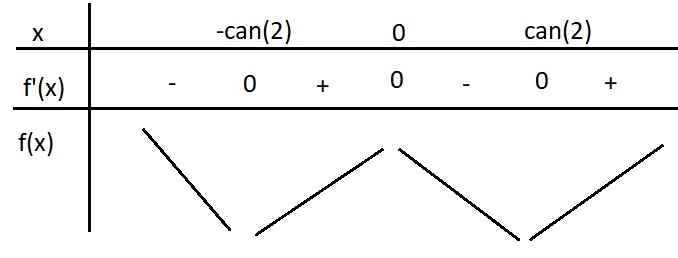
Hàm đồng biến trên các khoảng \(\left(-\sqrt{2};0\right)\cup\left(\sqrt{2};+\infty\right)\)
Hàm nghịch biến trên \(\left(-\infty;-\sqrt{2}\right)\cup\left(0;\sqrt{2}\right)\)
s.
\(y'=8x^3+12x=0\Rightarrow x=0\)
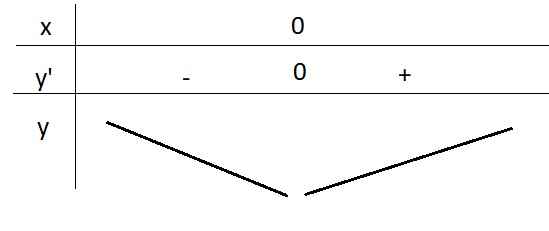
Hàm đồng biến trên \(\left(0;+\infty\right)\)
Hàm nghịch biến trên \(\left(-\infty;0\right)\)
cho hàm số y = 2x2 - (m - 1 )x +3, m là tham số
a. tìm khoảng đồng biến, nghịch biến của hàm số
b/ tìm các giái trị của m để hàm số đồng biến trên khoảng 1;+∞
c. tìm m để hàm số nghịch biến trên khoàng -4;8
d. tìm m để giá trị nhỏ nhất của hàm số là 9

Tìm các khoảng đồng biến- nghịch biến của hàm số.
TXĐ: \(D=\left[-1;1\right]\)
\(y'=\dfrac{-\dfrac{x\left(x+2\right)}{\sqrt{1-x^2}}-\sqrt{1-x^2}}{\left(x+2\right)^2}=\dfrac{-\left(2x+1\right)}{\left(x+2\right)^2\sqrt{1-x^2}}=0\Rightarrow x=-\dfrac{1}{2}\)
Dấu của y':
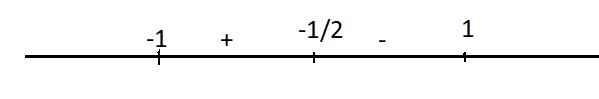
Hàm đồng biến trên \(\left(-1;-\dfrac{1}{2}\right)\) và nghịch biến trên \(\left(-\dfrac{1}{2};1\right)\)

Tìm các khoảng đồng biến- nghịch biến của hàm số.
ĐKXĐ: \(-3x^2+6x-3\ge0\Leftrightarrow-3\left(x-1\right)^2\ge0\)
\(\Leftrightarrow x=1\)
Miền xác định của hàm số có đúng 1 giá trị x nên hàm là hàm hằng \(y=0\), không đồng biến cũng không nghịch biến

Tìm các khoảng đồng biến- nghịch biến của hàm số.
TXĐ: \(D=(-\infty;0]\cup[6;+\infty)\)
\(y'=\sqrt{x^2-6x}+\dfrac{\left(x-3\right)\left(x-3\right)}{\sqrt{x^2-6x}}=\dfrac{2x^2-12x+9}{\sqrt{x^2-6x}}\)
\(\Rightarrow y'>0\) ; \(\forall x\in D\) hay hàm đồng biến trên các khoảng xác định
Vậy hàm đồng biến trên các khoảng \((-\infty;0]\) và \([6;+\infty)\)
Tìm các khoảng đồng biến, nghịch biến của các hàm số: y = 2 x x 2 - 9
TXĐ: R \ {-3; 3}
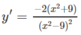
y' < 0 trên các khoảng (- ∞ ; - 3), (-3; 3), (3; + ∞ ) nên hàm số đã cho nghịch biến trên các khoảng đó.
Tìm các khoảng đồng biến, nghịch biến của các hàm số: y = 1 x - 5 2
TXĐ: R \ {5}
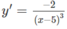
y' < 0 trên khoảng (5; + ∞ ) nên y nghịch biến trên khoảng (5; + ∞ )
y' > 0 trên khoảng (- ∞ ; 5) nên y đồng biến trên khoảng (- ∞ ; 5)
Tìm các khoảng đồng biến, nghịch biến của các hàm số: y = x 4 + 48 x
TXĐ: R \ {0}
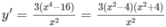
y' = 0 ⇔ 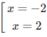
Bảng biến thiên:
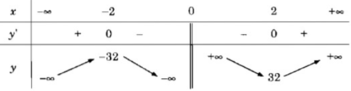
Vậy hàm số đã cho đồng biến trên các khoảng (- ∞ ; -2), (2; + ∞ ) và nghịch biến trên các khoảng (-2; 0), (0; 2)
Tìm các khoảng đồng biến, nghịch biến của các hàm số: y = 3 - 2 x x + 7
TXĐ: R \ {-7}
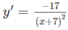
y' < 0 trên các khoảng (- ∞ ; -7), (-7; + ∞ ) nên hàm số nghịch biến trên các khoảng đó