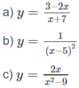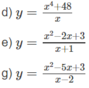a) TXĐ: R \ {-7}

y' < 0 trên các khoảng ( - ∞ ; -7), (-7; + ∞ ) nên hàm số nghịch biến trên các khoảng đó
b) TXĐ: R \ {5}
![]()
y' < 0 trên khoảng (5; + ∞ ) nên y nghịch biến trên khoảng (5; + ∞ )
y' > 0 trên khoảng ( - ∞ ; 5) nên y đồng biến trên khoảng ( - ∞ ; 5)
c) TXĐ: R \ {-3; 3}
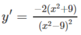
y' < 0 trên các khoảng ( - ∞ ; - 3), (-3; 3), (3; + ∞ ) nên hàm số đã cho nghịch biến trên các khoảng đó.
d) TXĐ: R \ {0}
![]()
y' = 0 ⇔ 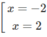
Bảng biến thiên:
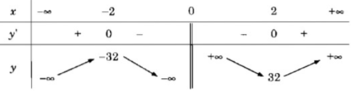
Vậy hàm số đã cho đồng biến trên các khoảng (-∞; -2), (2; +∞) và nghịch biến trên các khoảng (-2; 0), (0; 2)
e) TXĐ: R \ {-1}
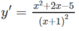
y' = 0 ⇔ 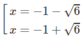

Vậy hàm số đã cho đồng biến trên các khoảng ( - ∞ ; −1 − √6), (−1 + √6; + ∞ ) và nghịch biến trên các khoảng (−1 − √6; −1),(−1; −1 + √6)
g) TXĐ: R \ {2}

(do x2 − 4x + 7x2 − 4x + 7 có Δ' = - 3 < 0)
Vậy hàm số đã cho đồng biến trên các khoảng (−∞;2),(2;+∞)