Cho hình vuông ABCD, tính cos A B → , C A →
A. 0,5
B. -0,5
C. 2 2
D. - 2 2
cho hình thang ABCD , AD=BC , AC vuông góc với BC, AD=5a,AC=12a,
a, Tính \(\frac{\sin B+\cos B}{\sin B-\cos B}\)
b, Tính chiều cao của hình thang
- giúp mình vs nà :*
cho hình thang ABCD , AD=BC , AC vuông góc với BC, AD=5a,AC=12a,
a, Tính \(\frac{\sin B+\cos B}{\sin B-\cos B}\)
b, Tính chiều cao của hình thang
Cho hình thang ABCD có hai cạnh bên là AD và BC bằng nhau, đường chéo AC vuông góc với cạnh bên BC. Biết AD = 5a, AC = 12 a
a) Tính :
\(\dfrac{\sin B+\cos B}{\sin B-\cos B}\)
b) Tính chiều cao của hình thang ABCD
a, \(\Delta ABC\) có \(\widehat{C}=90^o\).
Áp dụng pytago có: \(AB=\sqrt{AC^2+BC^2}=\sqrt{\left(12a\right)^2+\left(5a\right)^2}=13a\)
\(\Delta ABC\) có \(\widehat{C}=90^o\)\(\Rightarrow\)\(\left\{{}\begin{matrix}\sin B=\dfrac{AC}{AB}=\dfrac{12a}{13a}=\dfrac{12}{13}\\cosB=\dfrac{BC}{AB}=\dfrac{5a}{13a}=\dfrac{5}{13}\end{matrix}\right.\)
Ta có: \(\dfrac{sinB+cosB}{sinB-cosB}=\dfrac{\dfrac{12}{13}+\dfrac{5}{13}}{\dfrac{12}{13}-\dfrac{5}{13}}=\dfrac{\dfrac{17}{13}}{\dfrac{7}{13}}=\dfrac{17}{7}\)
b, Có SABCD= \(\dfrac{CH.AB}{2}=\dfrac{CB.AC}{2}\Rightarrow CH.AB=BC.AC\Rightarrow CH=\dfrac{AC.BC}{AB}=\dfrac{12a.5a}{13a}=\dfrac{60a}{13}\approx4,615a\)
Cho hình chóp S.ABCD có SA vuông góc (ABCD), ABCD là hình chữ nhật. AB=a, \(AD=a\sqrt{3}\). Biết rằng mp(SDC) tạo với đáy một góc bằng 60 độ.
a. Tính \(cos\left(\widehat{\left(SBC\right);\left(ABCD\right)}\right)\)
b: Tính \(tan\left(\widehat{\left(SBD\right);\left(ABCD\right)}\right)\)
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\AD\perp CD\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\)
Mà CD là giao tuyến (SCD) và (ABCD)
\(\Rightarrow\widehat{SDA}\) là góc giữa (SCD) và (ABCD)
\(\Rightarrow\widehat{SDA}=60^0\Rightarrow SA=AD.tan60^0=3a\)
a.
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
Mà \(BC=\left(SBC\right)\cap\left(ABCD\right)\Rightarrow\widehat{SBA}\) là góc giữa (SBC) và (ABCD)
\(tan\widehat{SBA}=\dfrac{SA}{AB}=3\Rightarrow\widehat{SBA}=...\)
b.
Từ A kẻ \(AE\perp BD\)
\(SA\perp\left(ABCD\right)\Rightarrow SA\perp BD\)
\(\Rightarrow BD\perp\left(SAE\right)\Rightarrow\widehat{SEA}\) là góc giữa (SBD) và (ABCD)
Hệ thức lượng: \(\dfrac{1}{AE^2}=\dfrac{1}{AB^2}+\dfrac{1}{AD^2}\Rightarrow AE=\dfrac{a\sqrt{3}}{2}\)
\(tan\widehat{SEA}=\dfrac{SA}{AE}=2\sqrt{3}\Rightarrow\widehat{SEA}=...\)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SAB là tam giác đều và (SAB) vuông góc với (ABCD). Tính cos φ với φ là góc tạo bởi (SAC) và (SCD).
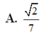
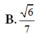
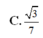
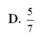
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SAB là tam giác đều và (SAB) vuông góc với (ABCD). Tính cos φ với φ là góc tạo bởi (SAC) và (SCD).
A. 2 7
B. 6 7
C. 3 7
D. 5 7
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Tam giác SAB là tam giác đều, mặt phẳng SAB vuông góc với mặt phẳng ABCD. Gọi b là góc giữa mặt phẳng SAC và mặt phẳng SCD. Tính Cos b
Cho hình vuông ABCD có cạnh bằng a, M là trung điểm của BC. Tính giá trị đúng của cos AMD.
Theo định lý cosin ta có
\(AD^2=AM^2+MD^2-2.MA.MD.cos\widehat{ÀMD}\)
Xé \(\Delta ABM\)có \(BM=\frac{a}{2}\)
\(AM=\sqrt{AB^2+BM^2}=\sqrt{a^2+\left(\frac{a}{2}\right)^2}=\frac{\sqrt{5}a}{2}\)
Xét \(\Delta DCM\)có \(CM=\frac{a}{2}\)
\(\Rightarrow DM=\sqrt{DC^2+CM^2}=\sqrt{a^2+\left(\frac{a}{2}\right)^2}=\frac{\sqrt{5}a}{2}\)
\(\Rightarrow\cos\widehat{AMD}=\frac{AM^2+MD^2-AD^2}{2.MA.MD}=\frac{\frac{5a^2}{4}+\frac{5a^2}{4}-a^2}{\frac{\sqrt{5}a}{2}.\frac{\sqrt{5}a}{2}}=\frac{3}{5}\)
Vậy \(\cos\widehat{AMD}=\frac{3}{5}\)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, cạnh SA vuông góc với mặt phẳng (ABCD), SA = AB = a , AD = 3 a . Gọi M là trung điểm BC. Tính cos góc tạo bởi hai mặt phẳng (ABCD) và (SDM).
A . 6 7 .
B . 5 7 .
C . 3 7 .
D . 1 7 .
Chọn A.
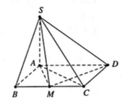
Gắn tọa độ Oxyz, với A(0;0;0), B(1;0;0), D(0;3;0), S(0;0;1)
Khi đó C ( 1 ; 3 ; 0 ) ⇒ Trung điểm M của BC là M ( 1 ; 3 2 ; 0 ) .
Ta có
SM → = ( 1 ; 3 2 ; - 1 ) , SD → = ( 0 ; 3 ; - 1 ) ⇒ [ SM → ; SD → ] = ( 3 2 ; 1 ; 3 ) .
Suy ra n ⃗ ( SDM ) = ( 3 2 ; 1 ; 3 ) mà n ⃗ ( ABCD ) = n ⃗ ( Oxy ) = ( 0 ; 0 ; 1 ) ,
ta được
cos ( SDM ^ ) ; ( ABCD ) = n → ( SDM ) . n → ( ABCD ) n → ( SDM ) . n → ( ABCD ) = 6 7 .