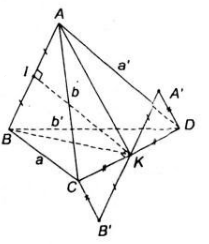
Chứng minh rằng nếu tứ diện ABCD có AB ⊥ CD và AC ⊥ BD thì AD ⊥ BC.
PB
Những câu hỏi liên quan
Chứng minh rằng nếu đường thẳng nối trung điểm hai cạnh AB và CD của tứ diện ABCD là đường vuông góc chung của AB và CD thì AC = BD và AD = BC.
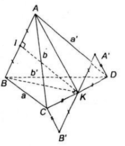
Gọi I, K lần lượt là trung điểm của cạnh AB và CD
Qua K kẻ đường thẳng d // AB, trên d lấy A', B' sao cho K là trung điểm của A'B' và
KA' = IA
* Xét tam giác CKB’ và DKA’ có:
KC= KD ( giả thiết)
KB’= KA’( cách dựng)
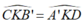 ( hai góc đối đỉnh )
( hai góc đối đỉnh )
=> ∆ CKB’ = ∆ DKA’ ( c.g.c)
=> B’C = A’D
*Xét tứ giác IBB’K có IB= KB’ và IB // KB’ ( cách dựng)
=> Tứ giác IBB’K là hình bình hành
=> BB’ // IK (1)
Chứng minh tương tự, ta có: AA’// IK (2)
Từ (1) và (2) suy ra: BB’// IK// AA’ (*)
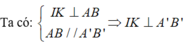
Lại có:IK ⊥ CK
=> IK ⊥ (CKB') (**)
Từ (*) và (**) suy ra BB' ⊥ (CKB') ; AA' ⊥ (CKB')
⇒ BB' ⊥ B'C; AA' ⊥ A'D
* Xét hai tam giác vuông BCB’ và ADA’ có:
BB’ = AA’ (= IK)
CB’ = A’D (chứng minh trên)
=> ∆ BCB’ = ∆ ADA’ ( cạnh huyền –cạnh góc vuông)
=> BC= AD.
* Chứng minh tương tự, AC = BD
Đúng 0
Bình luận (0)
Chứng minh rằng nếu đường thẳng nối trung điểm hai cạnh AB và CD của tứ diện ABCD là đường vuông góc chung của AB và CD thì AC = BD và AD = BC
Cho hình thang ABCD có AB // CD. Chứng minh rằng: Nếu AD+AC=BC+BD thì tứ giác ABCD là hình thang cân
cần gấp lắm hộ mình
Chứng minh rằng nếu tứ diện ABCD có \(AB\perp CD\) và \(AC\perp BD\) thì \(AD\perp BC\) ?
Cho hình thang ABCD (AB//CD). Chứng minh rằng nếu AD+AC=BC+BD thì tứ giác ABCD là hình thang cân. Giúp mình gấp với.
Cho tứ diện ABCD. Nếu AB ⊥CD, AC ⊥ BD và BC ⊥ AD thì: A.
A
B
→
.
A
C
→
≠
A
C
→
.
A
D
→
...
Đọc tiếp
Cho tứ diện ABCD. Nếu AB ⊥CD, AC ⊥ BD và BC ⊥ AD thì:
A. A B → . A C → ≠ A C → . A D → = A B → . A D →
B. A B → . A C → = A C → . A D → ≠ A B → . A D →
C. A B → . A C → = A C → . A D → = A B → . A D →
D. A B → . A C → ≠ A C → . A D → ≠ A B → . A D →
Ta có: A B → . C D → = A C → . B D → = A D → . C B → = 0
⇒ A B → ( A D → - A C → ) = A C → ( A D → - A B → ) = A D → ( A B → - A C → ) = 0
⇒ A B → . A C → = A C → . A D → = A B → . A D →
Đáp án C
Đúng 0
Bình luận (0)
Cho tứ diện ABCD, biết BD vuông góc với AC và CD vuông góc với AB. Chứng minh rằng AD vuông góc với BC.
(Vẽ hình: A là đỉnh của tứ diện, BCD là đáy của tứ diện)
+ Trên mặt phẳng đáy BCD kẻ các đường cao của tam giác BCD là BE, CF, DK.Ba đường cao gặp nhau tại H.
+ Xét mặt phẳng ABE
CD vuông góc BE
CD vuông góc AB
=> CD vuông góc với mặt phẳng ABE => CD vuông góc với AH (1)
+ Xét mặt phẳng ACF
BD vuông góc AC
BD vuông góc CF
=> BD vuông góc với mặt phẳng ACF => BD vuông góc với AH (2)
+ Từ (1) và (2) => AH vuông góc BCD
=> AH vuông góc với BC
Mà BC vuông góc với DK
=> BC vuông góc với mp ADK => BC vuông góc với AD
Đúng 0
Bình luận (0)
Cho tứ giác ABCD có P và Q là trung điểm của AB và CD, M và N là trung điểm của các đường chéo AC và BD. AC và BD cắt nhau tại H.
Chứng minh rằng:
a) Nếu MN vuông góc với PQ thì BC và AD bằng nhau.
b)Nếu bốn tam giác AHB, BHC, CHD và DHA có diện tích bằng nhau thì ABCD là hình bình hành.
Cho tứ diện ABCD. Chứng minh rằng:
\(\left(AB+CD\right)^2+\left(AD+BC\right)^2>\left(AC+BD\right)^2\)