Giúp e bài này vs thầy Nguyễn Việt Lâm ơi!!!Khó quas ạ!!)
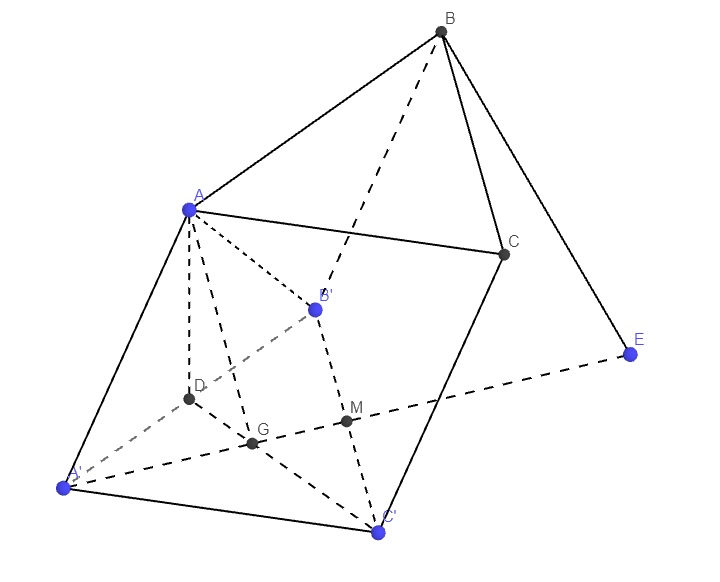
Cho hình lăng trụ ABC.A'B'C' có đáy ABC là tam giác cân tại C. Gọi G là trọng tâm tam giác A'B'C', E là điểm thỏa mãn: \(\overrightarrow{EA'}=3\overrightarrow{GA'}\). Biết rằng AA'=AB' và A'B'=2a. Khoảng cách giữa hai đường thẳng AG và BE là?
G là trọng tâm \(A'B'C'\Rightarrow\overrightarrow{A'G}=\dfrac{1}{3}\left(\overrightarrow{A'B'}+\overrightarrow{A'C'}\right)\)
\(\Rightarrow\overrightarrow{A'E}=3\overrightarrow{A'G}=\overrightarrow{A'B'}+\overrightarrow{A'C'}\)
\(\Rightarrow A'B'EC'\) là hình bình hành
\(\Rightarrow EC'\) song song và bằng A'B' nên EC' cũng song song và bằng AB
\(\Rightarrow ABEC'\) là hình bình hành
\(\Rightarrow BE||AC'\Rightarrow BE||\left(AGC'\right)\)
\(\Rightarrow d\left(AG;BE\right)=d\left(BE;\left(AGC'\right)\right)=d\left(B;\left(AGC'\right)\right)\)
Gọi D là trung điểm A'B' \(\Rightarrow C'D\perp A'B'\) (do tam giác ABC cân tại C nên A'B'C' cũng cân tại C') (1)
\(AA'=AB'\Rightarrow\Delta AA'B'\) cân tại A \(\Rightarrow AD\perp A'B'\) (2)
(1);(2)\(\Rightarrow A'B'\perp\left(AGC'\right)\)
Hay \(AB\perp\left(AGC'\right)\)
\(\Rightarrow\)\(d\left(B;\left(AGC'\right)\right)=AB=2a\)
(Giúp e bài này vs ạ!!!Khó quas.)
Cho hình lăng trụ ABCD.A'B'C'D' có đáy ABCD là hình thang, đáy lớn AB; AB=2CD=2a. Hình chiếu của D' trên mặt phẳng (ABCD) trùng với giao điểm O của AC và BD. Gọi G là trọng tâm tam giác ADD'. Biết hình lăng trụ trên có diện tích đáy bằng \(\dfrac{3a^2}{2}\) và đường cao bằng a. Tính khoảng cách giữa GO và BB'
Gọi H là trung điểm DD', qua G kẻ đường thẳng song song A'A cắt AD tại E và cắt A'D' tại N
Talet: \(\dfrac{DE}{EA}=\dfrac{HG}{GA}=\dfrac{1}{2}\) (t/c trọng tâm)
Do AB song song CD, Talet: \(\dfrac{OD}{OB}=\dfrac{CD}{AB}=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{DE}{DA}=\dfrac{OD}{OB}\Rightarrow OE||AB\)
Kéo dài OE cắt BC tại F, qua N kẻ đường thẳng song song AB cắt B'C' tại M
\(\Rightarrow\left(ABB'A'\right)||\left(EFMN\right)\Rightarrow d\left(GO;BB'\right)=d\left(\left(ABB'A'\right);\left(EFMN\right)\right)\)
Lại có \(\left(ABB'A'\right)||\left(CDD'C'\right)\) và \(\dfrac{BF}{CF}=\dfrac{AE}{DE}=2\)
\(\Rightarrow d\left(\left(ABB'A'\right);\left(EFMN\right)\right)=2d\left(\left(CDD'C'\right);\left(EFMN\right)\right)=2d\left(O;\left(CDD'C'\right)\right)\)
Từ O kẻ OI vuông góc CD (I thuộc CD), từ O kẻ OK vuông góc D'I (K thuộc D'I)
\(\Rightarrow OK\perp\left(CDD'C'\right)\Rightarrow OK=d\left(O;\left(CDD'C'\right)\right)\)
Gọi chiều cao hình thang là \(h\Rightarrow S_{ABCD}=\dfrac{1}{2}\left(AB+CD\right).h=\dfrac{3a^2}{2}\Rightarrow h=\dfrac{3a^2}{AB+CD}=a\)
Theo Talet: \(\dfrac{OI}{h}=\dfrac{ED}{AD}=\dfrac{1}{3}\Rightarrow OI=\dfrac{h}{3}=\dfrac{a}{3}\)
Hệ thức lượng: \(OK=\dfrac{OI.D'I}{\sqrt{OI^2+D'I^2}}=\dfrac{a\sqrt{10}}{10}\)
\(\Rightarrow d\left(GO;BB'\right)=2OK=\dfrac{a\sqrt{10}}{5}\)
(Giúp e bài này vs ạ. Khó quas!!!)
Cho lăng trụ ABC.A'B'C' có đáy ABC là tam giác vuông tại C và cạnh AC=2a. Hình chiếu của A' trên mặt phẳng (ABC) trùng với trung điểm H của AC. Biết góc giữa hai mặt phẳng (AA'B'B) và (AA'C'C) bằng 30 độ; góc giữa cạnh bên với mặt đáy bằng 60 độ. Tính khoảng cách giữa hai đường thẳng A'H và B'C
\(\left\{{}\begin{matrix}A'H\perp\left(ABC\right)\Rightarrow A'H\perp BC\\BC\perp AC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(ACC'A'\right)\)
\(\Rightarrow BC\perp A'A\)
Từ C kẻ \(CD\perp A'A\)
\(\Rightarrow A'A\perp\left(BCD\right)\)
\(\Rightarrow\widehat{BDC}\) là góc giữa (AA'B'C) và (AA'C'C) \(\Rightarrow\widehat{BDC}=30^0\)
\(A'H\perp\left(ABC\right)\Rightarrow\widehat{A'AH}\) là góc giữa cạnh bên và đáy
\(\Rightarrow\widehat{A'AH}=60^0\Rightarrow CD=AC.sin60^0=a\sqrt{3}\)
\(\Rightarrow B'C'=BC=CD.tan30^0=a\)
Gọi E là trung điểm A'C' \(\Rightarrow CE||A'H\Rightarrow CE\perp\left(A'B'C'\right)\)
\(A'H||\left(B'CE\right)\Rightarrow d\left(A'H;B'C\right)=d\left(A'H;\left(B'CE\right)\right)=d\left(A';\left(B'CE\right)\right)\)
Từ A' kẻ \(A'F\perp B'E\)
Do \(CE\perp\left(A'B'C'\right)\Rightarrow CE\perp A'F\)
\(\Rightarrow A'F\perp\left(B'CE\right)\Rightarrow A'F=d\left(A;\left(B'CE\right)\right)\)
\(B'C'=BC=a=\dfrac{A'C'}{2}=C'E\Rightarrow\Delta B'C'E\) vuông cân tại C'
\(\Rightarrow\widehat{B'EC'}=45^0\Rightarrow\widehat{A'EF}=\widehat{B'EC'}=45^0\) (đối đỉnh)
\(\Rightarrow A'F=A'E.sin45^0=\dfrac{a\sqrt{2}}{2}\)
(Giúp e bài này vs. Khó quas)
Cho hình hộp ABCD.A'B'C'D' có tất cả các cạnh bằng nhau và bằng a. Góc DAA' bằng góc A'AB bằng 60 độ, , góc BAD bằng 90 độ. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CC',DD'. Tính khoảng cách giữa MN và PQ.
\(\left\{{}\begin{matrix}PQ||\left(ABCD\right)\\MN\in\left(ABCD\right)\end{matrix}\right.\)
\(\Rightarrow d\left(PQ;MN\right)=d\left(PQ;\left(ABCD\right)\right)=d\left(Q;\left(ABCD\right)\right)=\dfrac{1}{2}d\left(\left(ABCD\right);\left(A'B'C'D'\right)\right)\)
Ta có: \(A'D=A'B=A'A=a\) (các tam giác DAA' và A'AB đều) (1)
Gọi H là hình chiếu vuông góc của A' lên (ABCD)
\(\Rightarrow AH=BH=DH\) (theo (1))
\(\Rightarrow H\) là tâm đường tròn ngoại tiếp ABD
\(\Rightarrow H\) là trung điểm BD (do tam giác ABD vuông tại A theo giả thiết)
\(\Rightarrow DH=\dfrac{1}{2}BD=\dfrac{1}{2}\sqrt{AB^2+AD^2}=\dfrac{a\sqrt{2}}{2}\)
\(\Rightarrow A'H=\sqrt{A'D^2-DH^2}=\dfrac{a\sqrt{2}}{2}\)
\(\Rightarrow d\left(MN;PQ\right)=\dfrac{1}{2}A'H=\dfrac{a\sqrt{2}}{4}\)
Cho hình chóp SABCD có đáy hình chữ nhật AB=a, BC=2a, SA vuông góc với ABCD, SA= acăn5. Tính khoảng cách từ C đến mp SAD.
Theo đề có:
\(\left\{{}\begin{matrix}CD\perp AD\\CD\perp SA\end{matrix}\right.\)
=> \(CD\perp\left(SAD\right)\)
<=> \(d\left(C,\left(SAD\right)\right)=CD=a\)
`HaNa♬`
Cho hình lăng trụ đều ABCA'B'C' có đáy =a ,(A'BC) tạo với đáy góc 45° . Điểm M nằm tùy ý M thuộc B'C' .Tính khoảng cách d(M,A'BC)
Cho hình chóp đều SABCD,AB=a SA=2a AC∩ BD=O. M,N,P là trung điểm của BC,CD và SA. Xác định d(A;(SBD)) Xác dịnh d(D;(SCD)) Xâc định d(O;(SMN)) Xác định d(O;(SAN))
Hãy giúp mình giải bài này với lời giải chi tiết và trình bày rõ ràng, mình cảm ơn ạ
Cho tứ diện đều ABCD cạnh a, có tâm của đáy là O. Tính khoảng cách:
a) Từ O đến (ACD)
b) Từ M đến (ABD) với M là trung điểm CD
c) Từ AB đến CD
Giải giúp mình câu này với ạ!! Cho hình chóp tứ giác đều S.ABCD, có các cạnh đều bằng a. Gọi O là tâm đáy và I là trung điểm của CD. Tính khoảng cách từ S đến CD.
Vì `SCD` cân tại `S=>SI \bot CD`
Trong `(SCD)` có: `SI \bot CD`
`=>d(S,CD)=SI=[a\sqrt{3}]/2`
1/ Cho hình chóp S.ABC: SA vuông góc với (ABC), ΔABC vuông tại B, AB=4a, BC=3a, SA=\(a\sqrt{2}\). H là chân d cao kẻ từ A xuống SA.
a. CMR: BC vuông góc với (SAB)
b. Tính d(B;(SAC))
c. Tính d(AH;SC)
2/ Cho hình chóp S.ABCD: ABCD là hình vuông tâm O. SO vuông góc với (ABCD), AB=2a, SO=4a
a. CMR: BD vuông góc với (SAC)
b. Tính d(O;(SCD))
c. Tính d(AB;SD)
CỨU E VS M.N ƠI, mai kt 15' nx mà thật sự ko bt lm, giúp e vs, cảm ơn ạ
1:
a: BC vuông góc BA
BC vuông góc SA
=>BC vuông góc (SAB)
b: Kẻ BK vuông góc AC, BH vuông góc SK
=>BH=d(B;(SAC))
\(AC=\sqrt{BA^2+BC^2}=5a\)
AK=(4a)^2/5a=3,2a
BK=4a*3a/5a=2,4a
\(SB=\sqrt{2a^2+16a^2}=3a\sqrt{2}\)
SK=căn 2a^2+10,24a^2=a*3căn 34/5
BK=2,4a
SK^2+BK^2=SB^2
nên ΔSKB vuông tại K
=>K trùng với H
=>d(B;(SAC))=BK=2,4a
