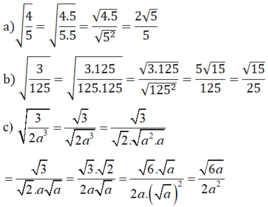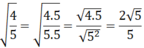Khử mẫu của biểu thức lấy căn 3 2 a 2 v ớ i a > 0
PB
Những câu hỏi liên quan
Khử mẫu của biểu thức lấy căn \(\sqrt{\dfrac{3}{\left(-4\right)^2}}\)
\(\sqrt{\dfrac{3}{\left(-4\right)^2}}=\dfrac{\sqrt{3}}{\sqrt{\left(-4\right)^2}}=\dfrac{\sqrt{3}}{4}\)
Đúng 0
Bình luận (0)
\(\sqrt{\dfrac{3}{\left(-4\right)^2}}=\dfrac{\sqrt{3}}{4}\)
Đúng 0
Bình luận (0)
1) thực hiện phép tính
\(3\sqrt{12}+\dfrac{1}{2}\sqrt{48}-\sqrt{27}\)
2) trục căn thức ở mẫu : \(\dfrac{2}{\sqrt{3}-5}\)
3) khử mẫu của biểu thức lấy căn: \(\sqrt{\dfrac{2}{5}}\)
1) Ta có: \(3\sqrt{12}+\dfrac{1}{2}\sqrt{48}-\sqrt{27}\)
\(=3\cdot2\sqrt{3}+\dfrac{1}{2}\cdot4\sqrt{3}-3\sqrt{3}\)
\(=6\sqrt{3}+2\sqrt{3}-3\sqrt{3}\)
\(=5\sqrt{3}\)
2) Ta có: \(\dfrac{2}{\sqrt{3}-5}\)
\(=\dfrac{2\left(\sqrt{3}+5\right)}{\left(\sqrt{3}-5\right)\left(\sqrt{3}+5\right)}\)
\(=\dfrac{2\left(\sqrt{3}+5\right)}{3-25}\)
\(=\dfrac{-2\left(\sqrt{3}+5\right)}{22}\)
\(=\dfrac{-\sqrt{3}-5}{11}\)
3) Ta có: \(\sqrt{\dfrac{2}{5}}\)
\(=\dfrac{\sqrt{2}}{\sqrt{5}}\)
\(=\dfrac{\sqrt{2}\cdot\sqrt{5}}{5}\)
\(=\dfrac{\sqrt{10}}{5}\)
Đúng 2
Bình luận (1)
Khử mẫu của biểu thức lấy căn
\(\sqrt{\dfrac{1}{b}+\dfrac{1}{b^2}}\)
(giả thiết các biểu thức có nghĩa)
\(=\sqrt{\dfrac{b+1}{b^2}}=\left[{}\begin{matrix}\dfrac{\sqrt{b+1}}{b}\left(b>0\right)\\-\dfrac{\sqrt{b+1}}{b}\left(-1\le b< 0\right)\end{matrix}\right.\)
Đúng 4
Bình luận (1)
khử mẫu của biểu thức lấy căn
\(\sqrt{\frac{\left(1+\sqrt{2}\right)^3}{27}}\)
Khử mẫu biểu thức chứa căn ms đúng
\(\sqrt{\frac{\left(1+\sqrt{2}\right)^3}{27}}=\sqrt{\frac{\left(1+\sqrt{2}\right)^2\cdot\left(1+\sqrt{2}\right)}{3^2\cdot3}}=\frac{1+\sqrt{2}}{3}\cdot\sqrt{\frac{1+\sqrt{2}}{3}}\)
\(=\frac{1+\sqrt{2}}{3}\cdot\frac{\sqrt{3\cdot\left(1+\sqrt{2}\right)}}{3}=\frac{1+\sqrt{2}}{9}\cdot\sqrt{3+3\sqrt{2}}\)
Đúng 0
Bình luận (0)
Khử mẫu của biểu thức lấy căn
a ) 4 5 ; b ) 3 125 c ) 3 2 a 2 v ớ i a > 0
Khử mẫu của biểu thức lấy căn
4 5
Khử mẫu của biểu thức lấy căn
1 600 ; 11 540 ; 3 50 ; 1 - 3 2 27
(Ghi nhớ: Khử căn ở mẫu tức là nhân cả tử và mẫu với thừa số có chứa căn.)
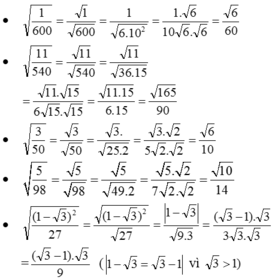
Đúng 0
Bình luận (0)
Khử mẫu của biểu thức lấy căn
1
600
;
11
540
;
3
50
;
5
98
;
1
-
3
2
27
Đọc tiếp
Khử mẫu của biểu thức lấy căn 1 600 ; 11 540 ; 3 50 ; 5 98 ; 1 - 3 2 27
(Ghi nhớ: Khử căn ở mẫu tức là nhân cả tử và mẫu với thừa số có chứa căn.)
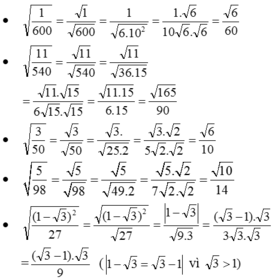
Đúng 0
Bình luận (0)
Khử mẫu của biểu thức lấy căn
\(\sqrt{\frac{\left(1+\sqrt{2}\right)^3}{27}}\)
Đưa 1 thừa số vào trong dấu căn
\(ab\sqrt{\frac{1}{a}+\frac{1}{b}}vớia>0,b>0\)
Lời giải:
\(\sqrt{\frac{(1+\sqrt{2})^3}{27}}=\sqrt{\frac{(1+\sqrt{2})^3}{3^3}}=\sqrt{\frac{3(1+\sqrt{2})^3}{3^4}}\)
\(=\frac{(1+\sqrt{2})\sqrt{3+3\sqrt{2}}}{9}\)
\(ab\sqrt{\frac{1}{a}+\frac{1}{b}}=\sqrt{(ab)^2(\frac{1}{a}+\frac{1}{b})}=\sqrt{ab^2+a^2b}\)