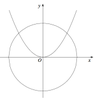
Biết rằng đường Parabol P : y 2 = 2 x chia đường tròn C : x 2 + y 2 = 8 thành hai phần lần lượt có diện tích là S 1 , S 2 (hình bên). Khi đó S 2 - S 1 = a π - b c với a, b, c nguyên dương và là phân số tối giản. Tổng a + b + c bằng
A. 13
B. 14
C. 15
D. 16






 .
.