Không dùng công thức nghiệm, tìm số nghiệm của phương trình -4 x 2 + 9 = 0
A. 0
B. 1
C. 3
D. 2
Không dùng công thức nghiệm, tìm số nghiệm của phương trình − 4 x 2 + 9 = 0
A. 0
B. 1
C. 3
D. 2
Ta có: −4x2 + 9 = 0 ⇔ 4x2 = 9
⇔ x 2 = 9 4 ⇔ x = 3 2 x = − 3 2
phương trình có hai nghiệm
x = 3 2 ; x = − 3 2
Đáp án cần chọn là: D
Không dùng công thức nghiệm, tìm số nghiệm của phương trình - 4 x 2 + 9 = 0
A. 0
B. 1
C. 3
D. 2
Đáp án D
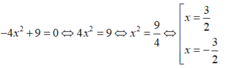
Nên số nghiệm của phương trình là 2.
Xác định a, b, b', c, dùng công thức nghiệm thu gọn giải các phương trình:
1)\(\dfrac{x^2}{9}-\dfrac{8x}{3}+16=0\)
2)\(0,4x^2-7x+30=0\)
Dùng công thức nghiệm,công thức nghiệm thu gọn giải các phương trình sau:
a.\(x^2-4x-21=0\)
b.\(4x^2+28x+49=0\)
c.\(6y^2-5\sqrt{2}y+2=0\)
d.\(y^2-\left(1+\sqrt{3}\right)y+\sqrt{3}=0\)
e.\(x^2+3x-10=0\)
a: =>(x-7)(x+3)=0
hay \(x\in\left\{7;-3\right\}\)
b: =>2x+7=0
hay x=-7/2
c: \(\Delta=50-4\cdot6\cdot2=50-48=2\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{5\sqrt{2}-\sqrt{2}}{12}=\dfrac{\sqrt{2}}{3}\\x_2=\dfrac{\sqrt{2}}{2}\end{matrix}\right.\)
Không dùng công thức nghiệm, tìm số nghiệm của phương trình − 9 x 2 + 30 x − 25 = 0
A. 0
B. 1
C. 3
D. 2
Ta có: −9x2 + 30x − 25 = 0
⇔ 9x2 − 30x + 25 = 0
⇔ (3x)2 – 2.3.5x + 52 = 0
⇔ (3x – 5)2 = 0 ⇔ 3x – 5 = 0
⇔ x = 5 3
Phương trình có một nghiệm x = 5 3
Đáp án cần chọn là: B
Dùng công thức nghiệm,giải các phương trình sau:
a. \(x^2+3x+4=0\)
b. \(4x^2-4x+1=0\)
c. \(x^2-5x-6=0\)
d. \(3x^2+12x-2=0\)
e. \(x^2+2\sqrt{5}x-1=0\)
f. \(2x^2-4\sqrt{2}x+2=0\)
Tìm m để các phương trình sau (dùng công thức nghiệm thu gọn)
a.\(x^2+2\left(m-2\right)x+m^2-3=0\) có nghiệm
b.\(\left(2m-1\right)x-4mx+2m+3=0\) có nghiệm kép
c.\(4x^2-2\left(2m-1\right)x+m^2=0\) vô nghiệm
a: \(\Leftrightarrow\left(2m-4\right)^2-4\left(m^2-3\right)>=0\)
\(\Leftrightarrow4m^2-16m+16-4m^2+12>=0\)
=>-16m>=-28
hay m<=7/4
b: \(\Leftrightarrow16m^2-4\left(2m-1\right)\left(2m+3\right)=0\)
\(\Leftrightarrow16m^2-4\left(4m^2+4m-3\right)=0\)
=>4m-3=0
hay m=3/4
c: \(\Leftrightarrow\left(4m-2\right)^2-4\cdot4\cdot m^2< 0\)
=>-16m+4<0
hay m>1/4
Câu 33 : số nghiệm của phương trình 3cos x + 2=0 trên đoạn [0;5π] là: A. 4 B. 3 C. 6 D. 5 Câu 34. Số nghiệm của phương trình ( 2cos^2 x - cos x)/ (tan x -√3)=0 trên đoạn [0;3] là A. 4 B. 3 C. 2 D. 1
Xác định a, b, b', c, dùng công thức nghiệm thu gọn giải các phương trình::
1) 4x2 - 9 = 0;
2) - 2x2 + 50 = 0;
3) 3x2 + 11 = 0
1) \(4x^2-9=0\)
Theo pt ta có: \(a=4;b=0;c=-9\)
\(\Delta=b^2-4ac=0^2-4.4.\left(-9\right)=144>0\)
=> Pt có 2 nghiệm phân biệt
\(x_1=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{-0-\sqrt{144}}{2.4}=-\dfrac{3}{2}\\ x_2=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{-0+\sqrt{144}}{2.4}=\dfrac{3}{2}\)
2) \(-2x^2+50=0\)
Theo pt ta có: \(a=-2;b=0;c=50\)
\(\Delta b^2-4ac=0^2-4.\left(-2\right).50=400>0\)
=> PT có 2 nghiệm phân biệt
\(x_1=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{-0-\sqrt{400}}{2.\left(-2\right)}=5\\ x_2=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{-0+\sqrt{400}}{2a}=-5\)
3) \(3x^2+11=0\)
Theo pt ta có: \(a=3;b=0;c=11\)
\(\Delta=b^2-4ac=0^2-4.3.11=-132< 0\)
=> PT vô nghiệm
1) 4x2 - 9 = 0
=>4x2=9
=>x2=9/4
=>x=\(\pm\dfrac{3}{2}\)
2) - 2x2 + 50 = 0
=>2x2=50
=>x2=25
=>x=\(\pm5\)
3) 3x2 + 11 = 0
=>3x2=-11
=>x2=-11/3(vo li)
=>x\(\in\phi\)
1) 4x2 - 9 = 0
Δ = b2 - 4ac = 02 - 4.4.(-9) = 144 > 0
=> pt đã cho có 2 nghiệm phân biệt :
x1 = \(\dfrac{\text{ −b+√Δ}}{2a}=\dfrac{-0+\sqrt{144}}{2.4}=\dfrac{3}{2}\)
x2 =\(\dfrac{\text{ −b−√Δ}}{2a}=\dfrac{-0-\sqrt{144}}{2.4}=-\dfrac{3}{2}\)
2) - 2x2 + 50 = 0
\(\Delta=b^2-4ac\) = 02 - 4.(-2).50 = 400 > 0
=> pt có 2 nghiệm phân biệt :
x1 = \(\dfrac{-b+\sqrt{\Delta}}{2.a}=\dfrac{-0+\sqrt{400}}{2.\left(-2\right)}=-5\)
x2 = \(\text{}\text{}\dfrac{-b-\sqrt{\Delta}}{2.a}=\dfrac{-0-\sqrt{400}}{2.\left(-2\right)}=5\)
3) 3x2 + 11 = 0
Δ = b2 - 4ac = 02 - 4.3.11 = -132 < 0
=> pt vô nghiệm