Chứng minh rằng với n ∈ N * , ta có đẳng thức: 2 + 5 + 8 + . . . + 3 n - 1 = n 3 n + 1 2
PB
Những câu hỏi liên quan
Chứng minh rằng với mọi số tự nhiên n ≥ 2 , ta có bất đẳng thức: 3 n > 3 n + 1
Chứng minh: 3n > 3n + 1 (1)
+ Với n = 2 thì (1) ⇔ 9 > 7 (luôn đúng).
+ Giả sử (1) đúng với n = k ≥ 2, tức là 3k > 3k + 1.
Ta chứng minh đúng với n= k+1 tức là chứng minh: 3k+ 1 > 3(k+1) + 1
Thật vậy, ta có:
3k + 1 = 3.3k > 3.(3k + 1) (Vì 3k > 3k + 1 theo giả sử)
= 9k + 3
= 3k + 3 + 6k
= 3.(k + 1) + 6k
> 3(k + 1) + 1.( vì k ≥ 2 nên 6k ≥ 12> 1)
⇒ (1) đúng với n = k + 1.
Vậy 3n > 3n + 1 đúng với mọi n ≥ 2.
Đúng 0
Bình luận (0)
Chứng minh rằng với
n
∈
N
*
, ta có đẳng thức:
1
2
+
1
4
+
1
8
+
.
.
.
+
1
2
n
2...
Đọc tiếp
Chứng minh rằng với n ∈ N * , ta có đẳng thức: 1 2 + 1 4 + 1 8 + . . . + 1 2 n = 2 n - 1 2 n
+ Với n = 1 :

Vậy (2) đúng với n = 1
+ Giả sử đẳng thức đúng với n = k, tức là: 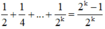
Cần chứng minh (2) đúng với n = k + 1, tức là: 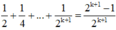
Thật vậy, ta có :
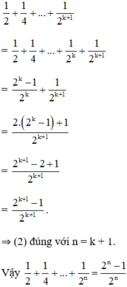
Đúng 0
Bình luận (0)
Chứng minh rằng với n ∈ N*, ta có đẳng thức:
1
2
+
2
2
+
3
2
+
.
.
.
.
+
n
2
n
n
+...
Đọc tiếp
Chứng minh rằng với n ∈ N*, ta có đẳng thức: 1 2 + 2 2 + 3 2 + . . . . + n 2 = n n + 1 2 n + 1 6
+ Với n = 1 :
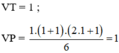
⇒ (3) đúng với n = 1
+ Giả sử đẳng thức (3) đúng với n = k nghĩa là :
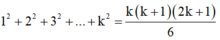
Cần chứng minh (3) đúng khi n = k + 1, tức là:
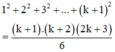
Thật vậy:
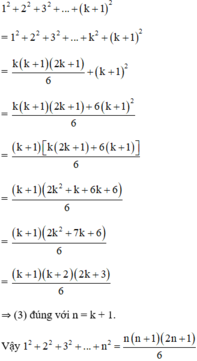
Đúng 0
Bình luận (0)
Chứng minh rằng với mọi số tự nhiên n ≥ 2 , ta có các bất đẳng thức: 2 n + 1 > 2 n + 3
2n + 1 > 2n + 3 (2)
+ Với n = 2 thì (2) ⇔ 8 > 7 (luôn đúng).
+ Giả sử (2) đúng khi n = k ≥ 2, nghĩa là 2k+1 > 2k + 3.
Ta chứng minh đúng với n= k+ 1 tức là chứng minh: 2k+2 > 2(k+ 1)+ 3
Thật vậy, ta có:
2k + 2 = 2.2k + 1
> 2.(2k + 3) = 4k + 6 = 2k + 2 + 2k + 4.
> 2k + 2 + 3 = 2.(k + 1) + 3 ( Vì 2k + 4 >3 với mọi k ≥ 2)
⇒ (2) đúng với n = k + 1.
Vậy 2n + 1 > 2n + 3 với mọi n ≥ 2.
Đúng 0
Bình luận (0)
Help
Chứng minh rằng với mọi số nguyên n≥2n≥2, ta luôn có đẳng thức sau :
(1−14)(1−19)...(1−1n2)=n+12n
Chứng minh rằng, với mọi số nguyên dương n ta luôn có bất đẳng thức
\(\frac{1}{6}+\frac{1}{12}+\frac{1}{20}+...+\frac{1}{n^2+3n+2}< \frac{1}{2}\)
\(\Leftrightarrow\frac{1}{6}+\frac{1}{12}+\frac{1}{20}+...+\frac{1}{n^2+n+2n+2}\)
\(\Leftrightarrow\frac{1}{2.3}+\frac{1}{3.4}+\frac{1}{4.5}+...+\frac{1}{\left(n+1\right).\left(n+2\right)}\)
\(\Leftrightarrow\frac{3-2}{2.3}+\frac{4-3}{3.4}+...+\frac{\left(n+2\right)-\left(n+1\right)}{\left(n+2\right).\left(n+1\right)}\)
\(\Leftrightarrow\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{x+1}-\frac{1}{x+2}\)
\(\Leftrightarrow\frac{1}{2}-\frac{1}{x+2}< \frac{1}{2}\left(đpcm\right)\)
Đúng 0
Bình luận (0)
Cho số nguyên dương n. Chứng minh rằng với mọi số thực dương x, ta có bất đẳng thức:
\(\frac{x^n\left(x^{n+1}+1\right)}{x^n+1}\le\left(\frac{x+1}{2}\right)^{2n+1}\)
Cho số nguyên dương n. Chứng minh rằng với mọi số thực dương x, ta có bất đẳng thức:
\(\frac{x^n\left(x^{x+1}+1\right)}{x^n+1}\le\left(\frac{x+1}{2}\right)^{2n+1}\)
a) 9x2 - 36
=(3x)2-62
=(3x-6)(3x+6)
=4(x-3)(x+3)
b) 2x3y-4x2y2+2xy3
=2xy(x2-2xy+y2)
=2xy(x-y)2
c) ab - b2-a+b
=ab-a-b2+b
=(ab-a)-(b2-b)
=a(b-1)-b(b-1)
=(b-1)(a-b)
P/s đùng để ý đến câu trả lời của mình
Đúng 0
Bình luận (0)
Chứng minh rằng với mọi số tự nhiên \(n\ge2\), ta có các bất đẳng thức :
a) \(3^n>3n+1\)
b) \(2^{n+1}>2n+3\)
a) Dễ thấy bất đẳng thức đúng với n = 2
Giả sử bất đẳng thức đúng với n = k ≥ 2, tức là
3k > 3k + 1
Nhân hai vế của (1) vơi 3, ta được:
3k + 1 > 9k + 3 <=> 3k + 1 > 3k + 4 + 6k -1.
Vì 6k - 1 > 0 nên
3k + 1 > 3k + 4 hay 3k + 1 > 3(k + 1) + 1.
tức là bất đẳng thức đúng với n = k + 1.
Vậy 3n > 3n + 1 với mọi số tự nhiên n ≥ 2.
b) Với n = 2 thì vế trái bằng 8, vế phải bằng 7. Vậy bất đẳng thức đúng với n = 2
Giả sử bất đẳng thức đúng với n = k ≥ 2, tức là
2k + 1 > 2k + 3 (2)
Ta phải chứng minh nó cũng đúng với n= k + 1, nghĩa là phải chứng minh
2k + 2 > 2(k + 1) + 3 <=> 2k + 2 > 2k + 5
Nhân hai vế của bất đẳng thức (2) với 2, ta được:
2k + 2 > 4k + 6 <=> 2k + 2 > 2k +5 + 2k + 1.
Vì 2k + 1> 0 nên 2k + 2 > 2k + 5
Vậy 2n + 1 > 2n + 3 với mọi số tự nhiên n ≥ 2.
Đúng 0
Bình luận (0)


