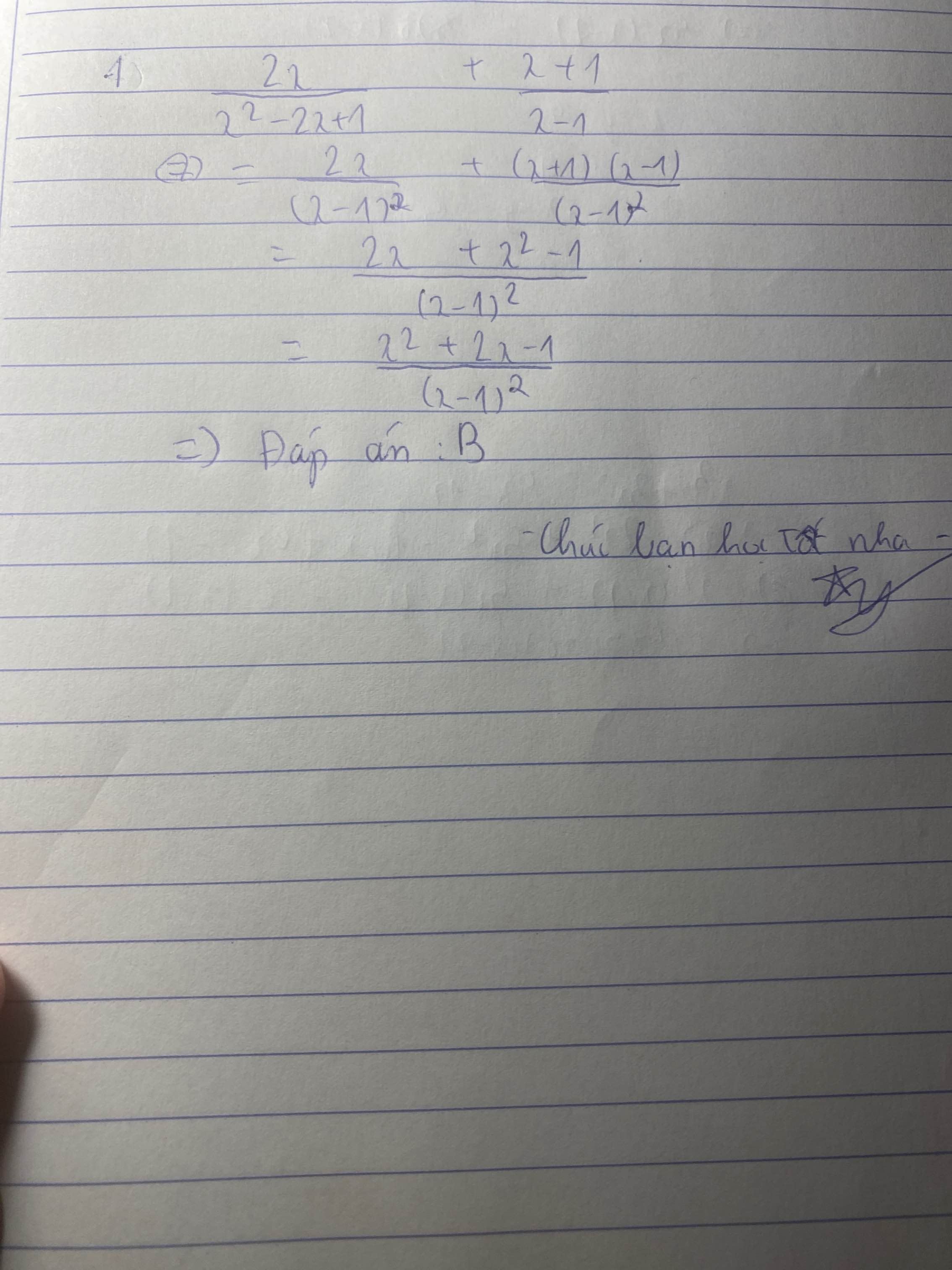Bài 1: Phương pháp quy nạp toán học

Giải giúp mình câu này với

Chứng minh bằng phương pháp quy nạp toán học:  \(\forall n\in N\)*, ta luôn có: \(sin^{2n}\alpha+cos^{2n}\alpha\le1\)

Chứng minh bằng phương pháp quy nạp toán học:  \(\forall n\in N\)*, n>1; ta có: \(\dfrac{1}{n+1}+\dfrac{1}{n+2}+...+\dfrac{1}{2n}>\dfrac{13}{24}\)

dùng quy nạp chứng minh 3 mũ n lớn hơn hoặc bằng 2n+1

1) hinh chu nhat co 2 duong..bang nhau la hinh vuong

A. Cheo          B. Trung binh     C. Canh doi            D. Canh ben

1) Hinh thoi ABCD co duong cheo AB < CD co may truc doi xung

A. 1    B. 2  C.3 D. 4

1) Thuc hien phep tinh cong 2 phan thuc \(\dfrac{2x}{x^2-2x+1}+\dfrac{x+1}{x-1}\) duoc ket qua la:

A. \(\dfrac{x^2+2x+1}{\left(x-1\right)^2}\)             B. \(\dfrac{x^2+2x-1}{\left(x-1\right)^2}\)      C. \(\dfrac{x^2-x-1}{\left(x-1\right)^2}\)           D. \(\dfrac{x^2-2x-1}{\left(x-1\right)^2}\)

1) Ket qua quy dong mau thuc cua 2 phan thuc \(\dfrac{1}{x-1}\) va \(\dfrac{2}{x+1}\)  la:

1) Ket qua khi rut gon phan thuc \(\dfrac{x^2+2x+1}{x^3+1}\) la:

1) Dieu kien cua x de phan thuc \(\dfrac{2x^3y^5}{5\left(x-2\right)^2}\) co nghia la

A. x ≠ 2              B. x ≠ -2

C. x = -2            D. x = 2