+ Với n = 1 :
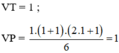
⇒ (3) đúng với n = 1
+ Giả sử đẳng thức (3) đúng với n = k nghĩa là :
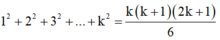
Cần chứng minh (3) đúng khi n = k + 1, tức là:
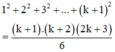
Thật vậy:
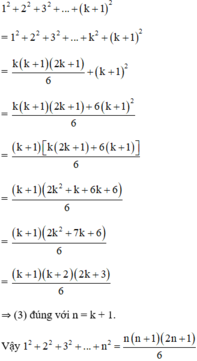
+ Với n = 1 :
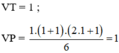
⇒ (3) đúng với n = 1
+ Giả sử đẳng thức (3) đúng với n = k nghĩa là :
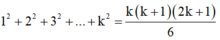
Cần chứng minh (3) đúng khi n = k + 1, tức là:
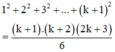
Thật vậy:
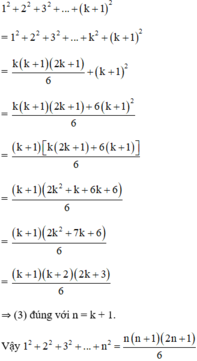
Chứng minh rằng với n ∈ N * , ta có đẳng thức: 2 + 5 + 8 + . . . + 3 n - 1 = n 3 n + 1 2
Help
Chứng minh rằng với mọi số nguyên n≥2n≥2, ta luôn có đẳng thức sau :
(1−14)(1−19)...(1−1n2)=n+12n
Chứng minh rằng với mọi số tự nhiên n ≥ 2 , ta có các bất đẳng thức: 2 n + 1 > 2 n + 3
Chứng minh rằng với mọi số tự nhiên n ≥ 2 , ta có bất đẳng thức: 3 n > 3 n + 1
Chứng minh các đẳng thức sau (với n∈N∗n∈N∗)
a) 2+5+8+...+(3n−1)=n(3n+1)22+5+8+...+(3n−1)=n(3n+1)2;
b) 3+9+27+...+3n=12(3n+1−3)3+9+27+...+3n=12(3n+1−3).
Chứng minh các bất đẳng thức sau 3n − 1 > n(n + 2) với n ≥ 4
Chứng minh đẳng thức sau ( v ớ i n ∈ N ∗ ) 2 + 5 + 8 + . . . + ( 3 n - 1 ) = 3 3 n + 1 2
Chứng minh rằng với mọi số tự nhiên n ≥ 2 , ta luôn có: 2 n + 1 > 2 n + 3 (*)
Chứng minh rằng với n ∈ N * thì 1 + 2 + 3 + . . . + n = n n + 1 2
chứng minh rằng với mọi số tự nhiên n>1,ta đều có \(\frac{4^n}{n+1}< \frac{\left(2n\right)!}{\left(n!\right)^2}\)