cho tam giác abc vuông tại a.đường cao ah.chứng minh.
a)ab2=bh.bc
b)ah2=bh.hc
Cho tam giác ABC vuông tại A, đường cao AH. Chứng minh
a) A B 2 = B H . B C ;
b) A H 2 = B H . H C .
a) Chứng minh được
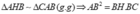
b) HS tự chứng minh
Cho tam giác ABC vuông tại A ; AB=3cm; AC=4cm ,Đường cao AH.
Chứng minh: a.AC2=BC.HC
b. AB.AC=BC.AH
c. AH2=BH.HC
a: Xét ΔABC vuông tại A có AH là đường cao
nên \(AC^2=HC\cdot BC\)(hệ thức lượng)
b: Xét ΔABC vuông tại A có AH là đường cao
nên \(AB\cdot AC=BC\cdot AH\)(hệ thức lượng)
c: Xét ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\)
Bài1. Cho tam giác ABC vuông tại A. Kẻ đường cao AH (H thuộc BC).
a) Tìm các cặp tam giác đồng dạng.
b) Chứng minh AH2=BH.CH; AB2 = BH.BC; AC2 = CH.BC
c) Biết BH=9cm, CH = 16cm. Tính độ dài các cạnh của tam giác ABC.
Cho tam giác ABC vuông tại A, đường cao AH.
a) Chứng minh A B 2 = B H . B C ; b) Chứng minh A H 2 = B H . C H ;
c) Gọi P là trung điểm của BH và Q là trung điểm của AH. Chứng minh Δ B A P ∽ Δ A C Q ;
d) Chứng minh A P ⊥ C Q .
Cho 🔺ABC vuông tại A.Đường cao AH.hãy chứng minh:
a) AB2 = BC.BH\(\)
AC2= BC.CH
b) AH2 = BH.HC
c) AH.BC = AB.AC
Chỉ mình với ~
cái này chỉ chứng minh các tam giác đồng dạng chứa các cạnh trên là ra thui
Cho tam giác ABC vuông ở A, đường cao AH. Chứng minh rằng:
a) Tam giác ABC đồng dạng với tam giác HBA;
b) AB BH.BC 2 ;
c) AH BH.HC 2 .
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
b: ΔBAC đồng dạng với ΔBHA
=>BA/BH=BC/BA
=>BA^2=BH*BC
c: Xét ΔHAC vuông tại H và ΔHBA vuông tại H có
góc HAC=góc HBA
=>ΔHAC đồng dạng với ΔHBA
=>HA/HB=HC/HA
=>HA^2=HB*HC
Cho tam giác ABC vuông tại A.Đường cao AH cắt đường phân giác BD tại I.CMR
a,IA.BH=IH.BA
b,AB2=HB.BC
c,HI/IA=AD/DC
chứng minh hộ mình câu a,c
a: Xét ΔBAH có BI là phân giác
nên IA/BA=IH/BH
=>IA*BH=BA*IH
c: HI/HA=BH/BA
AD/DC=BA/BC
mà BH/BA=BA/BC
nên HI/IA=AD/DC
Tam giác ABC vuông tại A, đường cao AH. HD vuông góc AB tại D, HE vuông góc AC tại E. a. Tứ giác ADHE lag hình gì?. b. Chứng minh: AH^2 = BH.HC, AB^2 = BH.BC
cho △ ABC ⊥ A, đường cao AH (H thuộc BC). Có △ABH đồng dạng △CBA, AB2 = BH.BC. Có △ABH đồng dạng △CAH ⇒AH2 = BH.CH
a) BD là tia phân giác của ∠ABC (D thuộc AC); Kẻ CI vuông góc BD (I thuộc BD). Chứng minh BD2= AB.BC - AD.CD
b) CI kéo dài cắt BA tại M; MD cắt BC tại K. Chứng minh \(\dfrac{DK}{\text{MK}}\)+\(\dfrac{DI}{\text{BI}}\)+\(\dfrac{DA}{\text{CA}}\)=1
Cho tam giác ABC vuông tai A (AB<AC) có duong cao AH.
a) Chung minh: tam giác HBA - tam giác HAC-tam giác ABC
b) Chung minh: *AB.AC=AH.BC
*AB2= BH.BC
*AC2= CH.CB
*HA2 =HB.HC
*1/AH2 = 1/AB2 + 1/AC2
c) ke HK vuông góc AB (K thuoc AB ), goi M,N lan luot là trung diem cua AC và HK. Chung minh B;N;M thang hàng.
a: Xét ΔHBA vuông tại H và ΔHAC vuông tại H có
góc HBA=góc HAC
=>ΔHBA đồng dạng với ΔHAC
Xét ΔHAC và ΔABC có
góc H=góc A
góc C chung
=>ΔHAC đồng dạngvới ΔABC
b: Xet ΔABC vuông tại A có AH vuông góc BC
nên AB*AC=AH*BC; AB^2=BH*BC; AC^2=CH*CB; HA^2=HB*HC; 1/AH^2=1/AB^2+1/AC^2