a) Chứng minh được
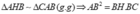
b) HS tự chứng minh
a) Chứng minh được
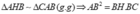
b) HS tự chứng minh
cho tam giác ABC vuông tại A vẽ đường cao AH,H thuốc BC.biết AB=6cm,AC= 8cm a. chứng minh tam giác HBA đồng dạng với với tam giác ABC b. tính BC,AH,BH c. kẻ HI vuông góc với AC tại I chứng minh HC^2=IC*AC
Cho tam giác ABC vuông tại A, đường trung tuy n AM, đường cao AH. Gọi D, E theo thứ
tự là chân đường vuông góc kẻ t H n AB, AC. Chứng minh rằng
a) AH = DE b) H ̂ B = M ̂ C
c) AM vuông góc DE
d) Chứng minh DICE là hình thang biết I l trung điểm của HB v K l trung điểm của HC
C1. Cho tam giác nhọn DEF. Đường cao EA và FB cắt nhau tại H.
a) Chứng minh rằng
b) Chứng minh rằng
C2. Cho tam giác nhọn ABC. Đường cao BD và CE cắt nhau tại H.
a) Chứng minh rằng
b) Chứng minh rằng
C3. Cho ABC vuông tại A, đư¬ờng cao AH cắt đ¬ường phân giác CD tại I.
a) Chứng minh rằng:
b) Chứng minh AC2 = CH.BC
C4. Cho hình bình hành ABCD, trên cạnh AB lấy một điểm M. Đường thẳng DM cắt cạnh CB kéo dài tại N.
a) Chứng minh : MAD MBN
b) Chứng minh : MA.MN = MD.MB
Cho tam giác ABC vuông tại A, đường cao AH (H thuộc BC) A. Chứng minh tam giác AHB đồng dạng với tam giác CAB B. Cho biết AB= 8cm, AC= 6cm. Tính độ dài AH, BH? C. Chứng minh AH²= HB.HC
cho tam giác ABC vuông tại a đường cao AH a) chứng minh tam giác ABC ~ tam giác HBA từ đó suy ra AB^2=BH .BC b) cho BH=4cm CH=9cm tính AH,AB c) gọi F điểm tùy ý trên AC, đường thẳng qua H vuông góc HF cắt cạnh AB tại E chứng minh AE . CH=AH . FC d) xác định vị trí của F trên AC để đoạn FE có độ dài ngắn nhất
Cho tam giác ABC vuông tại A, đường cao AH (H thuộc BC)
a) Chứng minh tam giác HBA đồng dạng với tam giác ABC
b) Chứng minh AH2 = HB . HC
c) Tia phân giác của góc AHC cắt AC tại D. Chứng minh HB/HC = AD^2/DC^2
Cho tam giác ABC vuông tại H có AH là đường cao (H thuộc BC) a) CMR tam giác ABC đồng dạng tam giác HAC b) Tính HC.BC=BC^2-AB^2
Cho tam giác ABC vuông tại A có đường cao AH, phân giác BD a) Chứng minh tam giác ABC đồng dạng tam giác HBA và AB^2 = BH .BC b) Giả sử AB = 6cm; AC = 8cm. Tính BC và AH. c) BD cắt AH tại E. Chứng minh AD.AE = CD.EH d) Lấy điểm K đối xứng với H qua A. Chứng minh rằng đường thẳng đi qua C và vuông góc với BK sẽ chia tam giác ACH thành hai phần có diện tích bằng nhau.
Cho tam giác ABC vuông tại A có đường cao AH, phân giác BD
a) Chứng minh tam giác ABC đồng dạng tam giác HBA và AB^2 = BH .BC
b) Giả sử AB = 6cm; AC = 8cm. Tính BC và AH.
c) BD cắt AH tại E. Chứng minh AD.AE = CD.EH
d) Lấy điểm K đối xứng với H qua A. Chứng minh rằng đường thẳng đi qua C và vuông góc với BK sẽ chia tam giác ACH thành hai phần có diện tích bằng nhau.
Cho tam giác ABC vuông tại A,đường cao AH (H thuộc BC) Biết AB=6cm,AC=8cm a c/m tam giác ABC đồng dạng tam giác HBA b Tính AH,BC