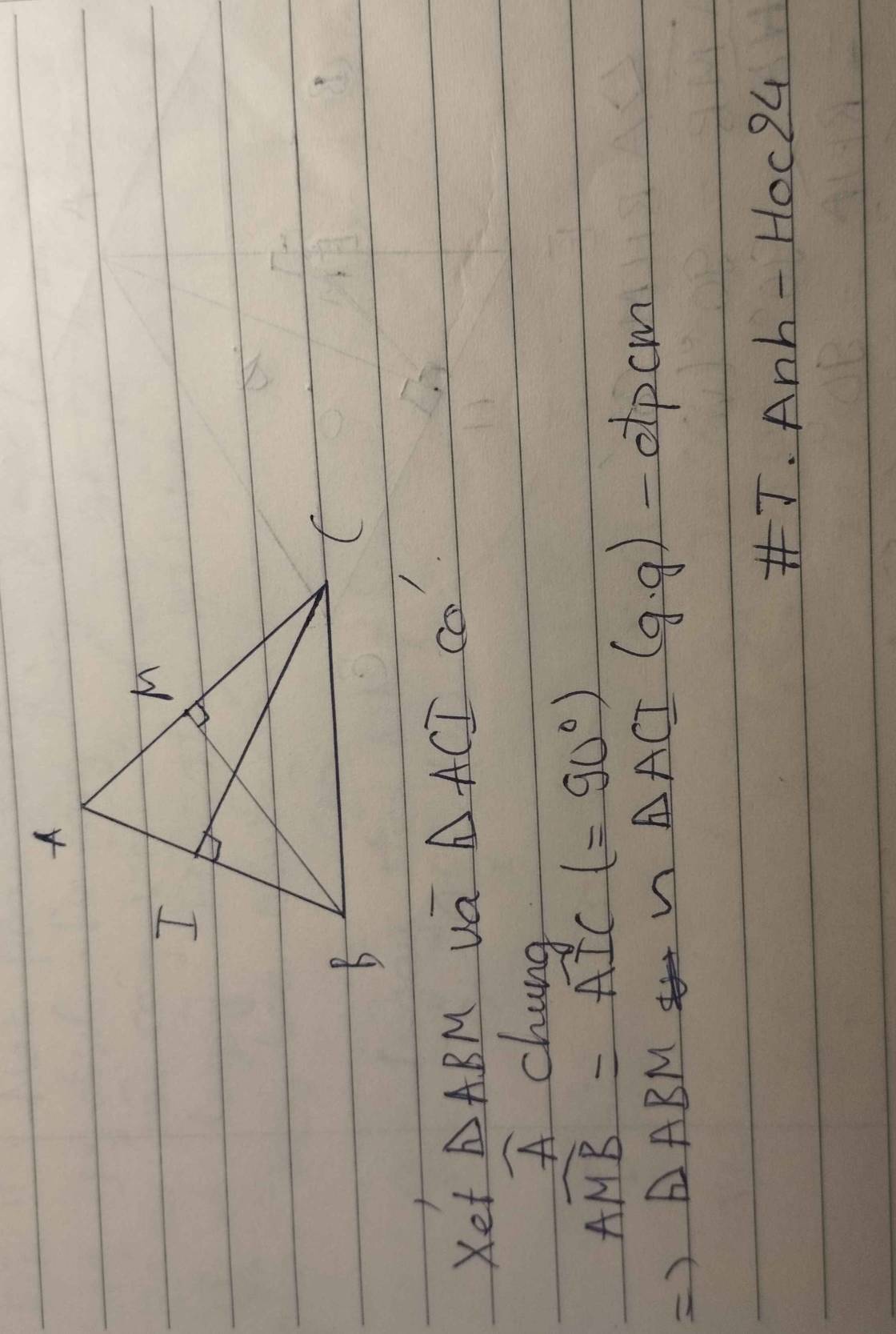Cho tam giác ABC vuông tại A. M bất kỳ trên cạnh BC. Trên tia đối tia MA lấy điểm D sao cho góc BDC vuông. CMR: BC.AD =AB.DC+AC.BD
Bài 8: Các trường hợp đồng dạng của tam giác vuông
Bài 4 tam giác ABC vuông tại A, AB 6 cm, AC 8 cm ,đường cao AH cắt phân giác BD tại I
a) Chứng minh tam giác ABC đồng dạng với tam giác HBA. Từ đó suy ra AB² BH.BC
b)Chứng minh IH/IA bằng AD/CD
c )Tính diện tích giác BCD
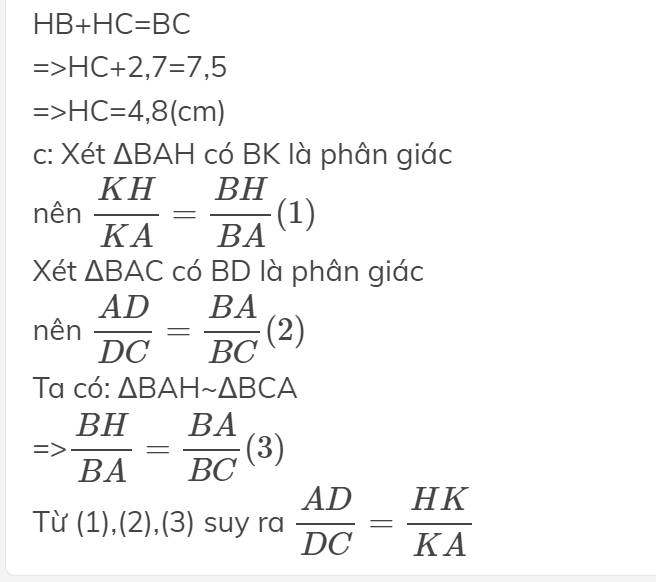
Bài 5 tam giác ABC vuông tại A ,AB 4,5 cm, BC 7,5 cm, đường cao AH, phân giác góc B cắt AC tại D và cắt AH tại K
a) chứng minh tam giác ABC đồng dạng tam giác HBA.Từ đó suy ra AB.AH AC.BH
b)tính AH, BH, CH
c) chứng minh KH/KA DA/DC
Bài 6 Cho hình chữ nhật ABCD ,AB...
Đọc tiếp
Bài 4 tam giác ABC vuông tại A, AB = 6 cm, AC = 8 cm ,đường cao AH cắt phân giác BD tại I a) Chứng minh tam giác ABC đồng dạng với tam giác HBA. Từ đó suy ra AB² = BH.BC b)Chứng minh IH/IA bằng AD/CD c )Tính diện tích giác BCD Bài 5 tam giác ABC vuông tại A ,AB = 4,5 cm, BC = 7,5 cm, đường cao AH, phân giác góc B cắt AC tại D và cắt AH tại K a) chứng minh tam giác ABC đồng dạng tam giác HBA.Từ đó suy ra AB.AH = AC.BH b)tính AH, BH, CH c) chứng minh KH/KA = DA/DC Bài 6 Cho hình chữ nhật ABCD ,AB = 4 cm ,AD = 3 cm ,đường cao AH của tam giác ADB a)chứng minh tam giác AHB đồng dạng tam giác BCD b) Chứng minh AB mũ 2 = DH.DB c)Tính DH,AH GIÚP MK VS Ạ ,MK ĐANG CẦN GẤP
Cho tam giác ABC vuông tại A, đường cao AH. Gọi M , N lần lượt là hình chiếu của H trên AB , AC .
a)AH.BC=AB.AC
b)△AMN~△ACB
HELP ME!!!!!!
a: ΔABC vuông tại A
=>\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\left(1\right)\)
Ta có: ΔABC có AH là đường cao
=>\(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC\left(2\right)\)
Từ (1) và (2) suy ra \(AB\cdot AC=AH\cdot BC\)
b: Xét ΔAMH vuông tại M và ΔAHB vuông tại H có
\(\widehat{MAH}\) chung
Do đó: ΔAMH~ΔAHB
=>\(\dfrac{AM}{AH}=\dfrac{AH}{AB}\)
=>\(AH^2=AM\cdot AB\left(3\right)\)
Xét ΔANH vuông tại N và ΔAHC vuông tại H có
\(\widehat{NAH}\) chung
Do đó: ΔANH~ΔAHC
=>\(\dfrac{AN}{AH}=\dfrac{AH}{AC}\)
=>\(AH^2=AN\cdot AC\left(4\right)\)
Từ (3) và (4) suy ra \(AM\cdot AB=AN\cdot AC\)
=>\(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
Xét ΔAMN và ΔACB có
\(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
\(\widehat{MAN}\) chung
Do đó: ΔAMN~ΔACB
Đúng 1
Bình luận (0)
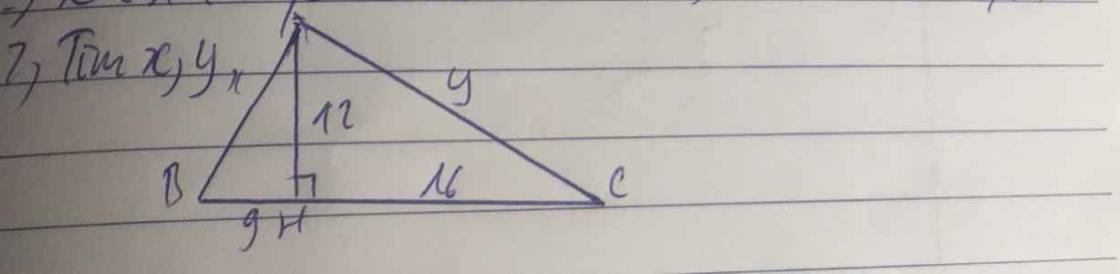 giúp mik vs định lí pythagore nhé tính x,y
giúp mik vs định lí pythagore nhé tính x,y
Vì `ΔBHA` vuông tại `H` nên áp dụng định lí Pythagore `:`
`BH^2 +AH^2 = AB^2`
`<=>9^2 + 12^2 = AB^2`
`<=>225=AB^2`
`=>AB = sqrt(225)=15`
Vì `ΔAHC` vuông tại `H` nên áp dụng định lí Pythagore `:`
`AH^2 + HC^2 = AC^2`
`<=> 12^2 + 16^2 = AC^2`
`<=>400=AC^2
`=>AC = sqrt(400)=20`
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH biết AB=15cm và AC=20cm a. Chứng minh rằng: AH.BC=AB.AC. Tính BC, AH b) Kẻ HM vuông góc AB, HN vuông góc AC. Chứng minh rằng tam giác AMN đồng dạng với tam giác ACB. c. Trung tuyến AK của tam giác ABC cắt MN tại I. Tính diện tích tam giác AMI
Xem chi tiết
a: Xét ΔABC có AH là đường cao
nên \(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC\left(1\right)\)
Ta có: ΔABC vuông tại A
=>\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\left(2\right)\)
Từ (1) và (2) suy ra \(AH\cdot BC=AB\cdot AC\)
Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=15^2+20^2=625\)
=>\(BC=\sqrt{625}=25\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot25=15\cdot20=300\)
=>\(AH=\dfrac{300}{25}=12\left(cm\right)\)
b: Xét ΔAHB vuông tại H có HM là đường cao
nên \(AM\cdot AB=AH^2\left(3\right)\)
Xét ΔAHC vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\left(4\right)\)
Từ (3) và (4) suy ra \(AM\cdot AB=AN\cdot AC\)
=>\(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
Xét ΔAMN vuông tại A và ΔACB vuông tại A có
\(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
Do đó: ΔAMN đồng dạng với ΔACB
c: Ta có: ΔABC vuông tại A
mà AK là đường trung tuyến
nên AK=KC=KB
Ta có: KA=KC
=>ΔKAC cân tại K
=>\(\widehat{KAC}=\widehat{KCA}\)
Ta có: ΔAMN đồng dạng với ΔACB
=>\(\widehat{ANM}=\widehat{ABC}\)
Ta có: \(\widehat{KAC}+\widehat{ANM}\)
\(=\widehat{ABC}+\widehat{KCA}=90^0\)
=>AK\(\perp\)MN tại I
Xét ΔABC vuông tại A có AH là đường cao
nên \(BH\cdot BC=BA^2;CH\cdot BC=CA^2\)
=>\(BH\cdot25=15^2=225;CH\cdot25=20^2=400\)
=>BH=225/25=9(cm); CH=400/25=16(cm)
Xét ΔAHB vuông tại H có HM là đường cao
nên \(AM\cdot AB=AH^2\)
=>\(AM\cdot15=12^2\)=144
=>AM=144/15=9,6(cm)
Ta có: AMHN là hình chữ nhật
=>AH=MN
mà AH=12cm
nênMN=12cm
Ta có: ΔANM vuông tại A
=>\(AN^2+AM^2=NM^2\)
=>\(AN^2+9,6^2=12^2\)
=>AN=7,2(cm)
Xét ΔIMA vuông tại I và ΔAMN vuông tại A có
\(\widehat{IMA}\) chung
Do đó: ΔIMA đồng dạng với ΔAMN
=>\(\dfrac{S_{IMA}}{S_{AMN}}=\left(\dfrac{AM}{MN}\right)^2=\left(\dfrac{4}{5}\right)^2=\dfrac{16}{25}\)
=>\(S_{IMA}=\dfrac{16}{25}\cdot\dfrac{1}{2}\cdot AM\cdot AN=22,1184\left(cm^2\right)\)
Đúng 1
Bình luận (1)
Bài 1. Cho tam giác ABC vuông tại A có AB = 6 cm, AC = 8 cm, NP = 5 cm và ABC ~
MNP. Khẳng định nào sau đây là sai:
A. NMP = 90
B. BC = 10 cm
C. MP = 4 cm.
D. MP = 3 cm.
giúp mik vs mik đang cần gấp
Cho x,y > 0 và 2x + y = 3 tìm Min B = x + 4y + 3/x + 5/y +2028 Giúp mình với ạ , cảm ơn bạn
Cho ∆ABC vuông tại A đường cao AH a) C/m ∆BAH đồng dạng ∆ACH b) C/m AH² = HB . HC c) Tính S∆BAH/S∆BCA biết AB = 6cm , AC = 8cm d) tia phân giác của góc B cắt AC tại M và cắt AH tại N . C/ m AM.AN = MC.NH Giúp mình bài này với ạ mình cần gấp , cảm ơn ạ!
a: Xét ΔBAH vuông tại H và ΔACH vuông tại H có
góc BAH=góc ACH
=>ΔHBA đồng dạg với ΔHAC
b: ΔHBA đồng dạng với ΔHAC
=>HB/HA=HA/HC
=>HA^2=HB*HC
c: BC=căn 6^2+8^2=10cm
Xét ΔBAH vuông tại H và ΔBCA vuông tại A có
góc B chung
=>ΔBAH đồng dạng với ΔBCA
=>S BAH/S BCA=(BA/BC)^2=9/25
Đúng 0
Bình luận (0)
Cho ∆ABC vuông tại A đường cao AH . Kẻ HE vuông góc với AC , Gọi K là giao điểm của AH và EB a)EH //AB b)Chứng minh ∆CAH đồng dạng ∆CBA c) Qua K kẻ đường thẳng // AB cắt AC tại M và cắt BC tại N . Chứng minh KM =KN d) Chứng minh CK đi qua trung điểm của AB
a: HE vuông góc AC
AB vuông góc AC
=>HE//AB
b: Xét ΔCAH vuông tại H và ΔCBA vuông tại A có
góc ACH chung
=>ΔCAH đồng dạng với ΔCBA
c: Xét ΔKEH và ΔKBA có
góc KEH=góc KBA
góc EKH=góc BKA
=>ΔKEH đồng dạng với ΔKBA
=>KE/KB=KH/KA
=>EK/EB=HK/HA
Xét ΔEAB có MK//AB
nên MK/AB=EK/EB
Xét ΔHAB có KN//AB
nên KN/AB=HK/HA
=>MK/AB=KN/AB
=>MK=KN
Đúng 0
Bình luận (1)
Cho △ABC, kẻ BM vuông góc với AC, kẻ CI vuông góc với AB. Chứng minh △ABM đồng dạng △ACI
Xét ΔABM vuông tại M và ΔACI vuông tại I có
góc BAM chung
=>ΔABM đồng dạng với ΔACI
Đúng 1
Bình luận (0)
Ta có:
`hat{BAM}=\hat{CAI}` (vì cả hai đều bằng góc nội tiếp cùng nhìn vào cung `AC`)
`hat{ABM}=hat{AIC}=90^o` (vì `BM` vuông góc với `AC` và `CI` vuông góc với `AB`)
Và `hat{BMA}=hat{CIA}` (vì chúng là các góc đối diện với cạnh `AB`)
`=>` Theo góc-góc, ta có `△ABM` đồng dạng `△ACI`
Đúng 1
Bình luận (0)