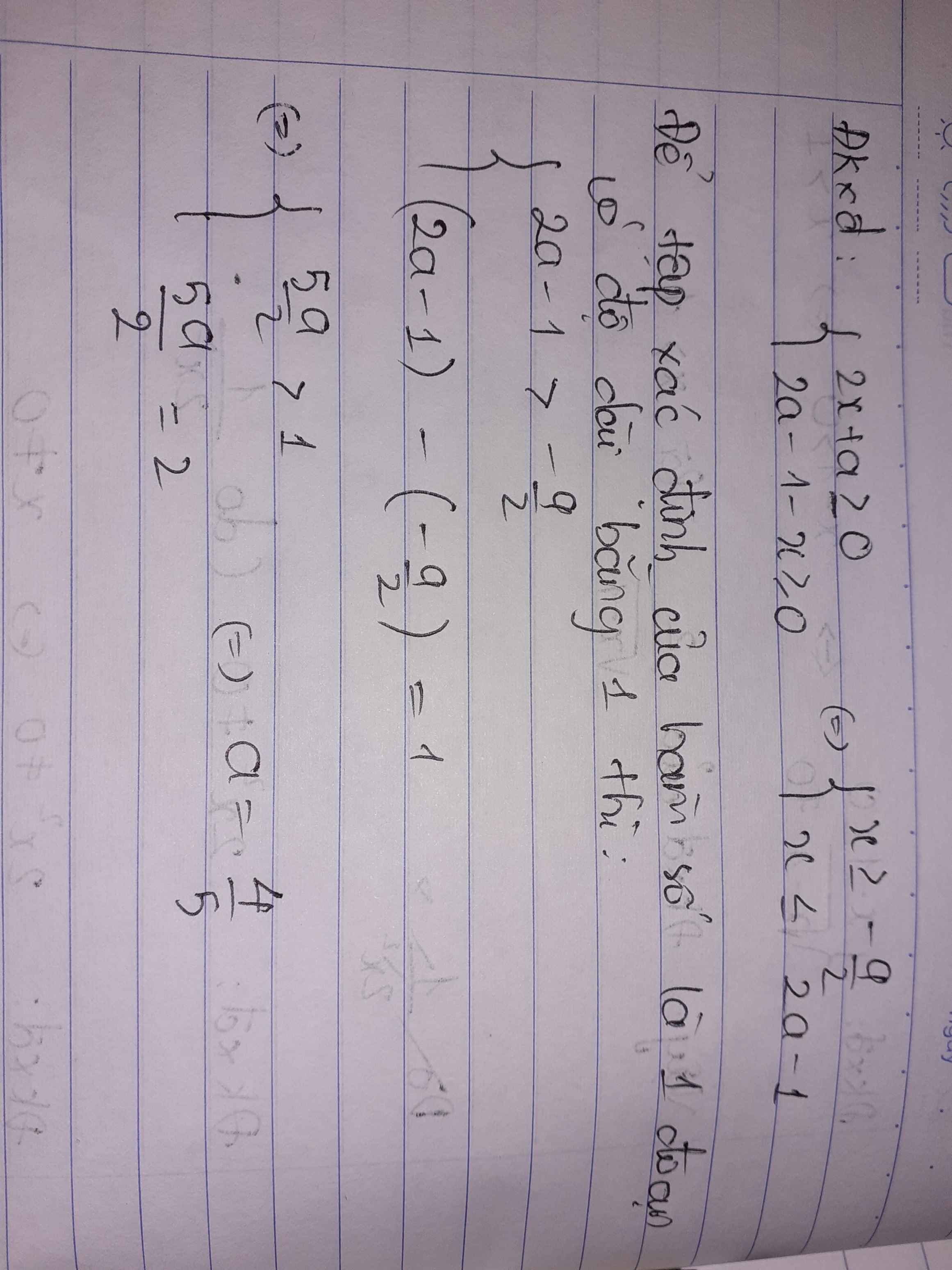a) Để K=R thì ta cần tìm A sao cho với mọi X\(\in R\)thì phân số đã cho xác định

ĐKXĐ : X² - 6X + A + 2 \(\ne\)0

Ta có : X² - 6X + A + 2 =0

\(\Delta\)=36 - 4A - 8

       =28 - 4A

mà  X² - 6X + A + 2 \(\ne\)0 nên 28-4A <0

=> A > 7

Bài 1: 

a) Để hàm số y=(k-2)x+k+3 là hàm số bậc nhất thì \(k\ne2\)

b) Để hàm số y=(k-2)x+k+3 đồng biến trên R thì k-2>0

hay k>2

Bài 2: 

Thay \(x=-\dfrac{1}{2}\) và \(y=\dfrac{2}{3}\) vào (D), ta được:

\(\left(2m-3\right)\cdot\dfrac{-1}{2}-\dfrac{1}{2}=\dfrac{2}{3}\)

\(\Leftrightarrow\left(2m-3\right)\cdot\dfrac{-1}{2}=\dfrac{2}{3}+\dfrac{1}{2}=\dfrac{7}{6}\)

\(\Leftrightarrow2m-3=\dfrac{7}{6}:\dfrac{-1}{2}=\dfrac{-7}{6}\cdot\dfrac{2}{1}=-\dfrac{14}{6}=-\dfrac{7}{3}\)

\(\Leftrightarrow2m=\dfrac{-7}{3}+3=\dfrac{-7}{3}+\dfrac{9}{3}=\dfrac{2}{3}\)

hay \(m=\dfrac{1}{3}\)

a) Để hàm số đồng biến thì k(k-3)>0

\(\Leftrightarrow\left[{}\begin{matrix}k>3\\k< 0\end{matrix}\right.\)

b) Để hàm số nghịch biến thì k(k-3)<0

hay 0<x<3

a) • \(y = f\left( x \right) = \frac{1}{{x - 1}}\)

ĐKXĐ: \(x - 1 \ne 0 \Leftrightarrow x \ne 1\)

Vậy hàm số có tập xác định: \(D = \mathbb{R}\backslash \left\{ 1 \right\}\).

• \(y = g\left( x \right) = \sqrt {4 - x} \)

ĐKXĐ: \(4 - x \ge 0 \Leftrightarrow x \le 4\)

Vậy hàm số có tập xác định: \(D = \left( { - \infty ;4} \right]\).

b) • Với mọi \({x_0} \in \left( { - \infty ;1} \right)\), ta có:

\(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{1}{{x - 1}} = \frac{{\mathop {\lim }\limits_{x \to {x_0}} 1}}{{\mathop {\lim }\limits_{x \to {x_0}} x - \mathop {\lim }\limits_{x \to {x_0}} 1}} = \frac{1}{{{x_0} - 1}} = f\left( {{x_0}} \right)\)

Vậy hàm số \(y = f\left( x \right)\) liên tục tại mọi điểm \({x_0} \in \left( { - \infty ;1} \right)\).

Tương tự ta có hàm số \(y = f\left( x \right)\) liên tục tại mọi điểm \({x_0} \in \left( {1; + \infty } \right)\).

Ta có: Hàm số không xác định tại điểm \({x_0} = 1\)

\(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \frac{1}{{x - 1}} =  + \infty ;\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ - }} \frac{1}{{x - 1}} =  - \infty \)

Vì \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) \ne \mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right)\) nên không tồn tại \(\mathop {\lim }\limits_{x \to 1} f\left( x \right)\).

Vậy hàm số \(y = f\left( x \right)\) không liên tục tại điểm \({x_0} = 1\).

• Với mọi \({x_0} \in \left( { - \infty ;4} \right)\), ta có:

\(\mathop {\lim }\limits_{x \to {x_0}} g\left( x \right) = \mathop {\lim }\limits_{x \to {x_0}} \sqrt {4 - x}  = \sqrt {\mathop {\lim }\limits_{x \to {x_0}} 4 - \mathop {\lim }\limits_{x \to {x_0}} x}  = \sqrt {4 - {x_0}}  = g\left( {{x_0}} \right)\)

Vậy hàm số \(y = g\left( x \right)\) liên tục tại mọi điểm \({x_0} \in \left( { - \infty ;4} \right)\).

Ta có: \(g\left( 4 \right) = \sqrt {4 - 4}  = 0\)

\(\mathop {\lim }\limits_{x \to {4^ - }} g\left( x \right) = \mathop {\lim }\limits_{x \to {4^ - }} \sqrt {4 - x}  = \sqrt {\mathop {\lim }\limits_{x \to {4^ - }} 4 - \mathop {\lim }\limits_{x \to {4^ - }} x}  = \sqrt {4 - 4}  = 0 = g\left( 4 \right)\)

Vậy hàm số \(y = g\left( x \right)\) liên tục tại điểm \({x_0} = 4\).

Hàm số không xác định tại mọi \({x_0} \in \left( {4; + \infty } \right)\) nên hàm số \(y = g\left( x \right)\) không liên tục tại mọi điểm \({x_0} \in \left( {4; + \infty } \right)\).

Vậy hàm số \(y = g\left( x \right)\) liên tục trên nửa khoảng \(\left( { - \infty ;4} \right]\).

mai em hk oy mong mọi người giúp ạ

ĐKXĐ: \(\left\{{}\begin{matrix}2x+a\ge0\\2a-1-x\ge0\end{matrix}\right.\) \(\Rightarrow-\dfrac{a}{2}\le x\le2a-1\)

Miền xác định là đoạn có độ dài 1 khi:

\(2a-1-\left(-\dfrac{a}{2}\right)=1\)

\(\Rightarrow a=\dfrac{4}{5}\)

\(a=\dfrac{4}{5}\)