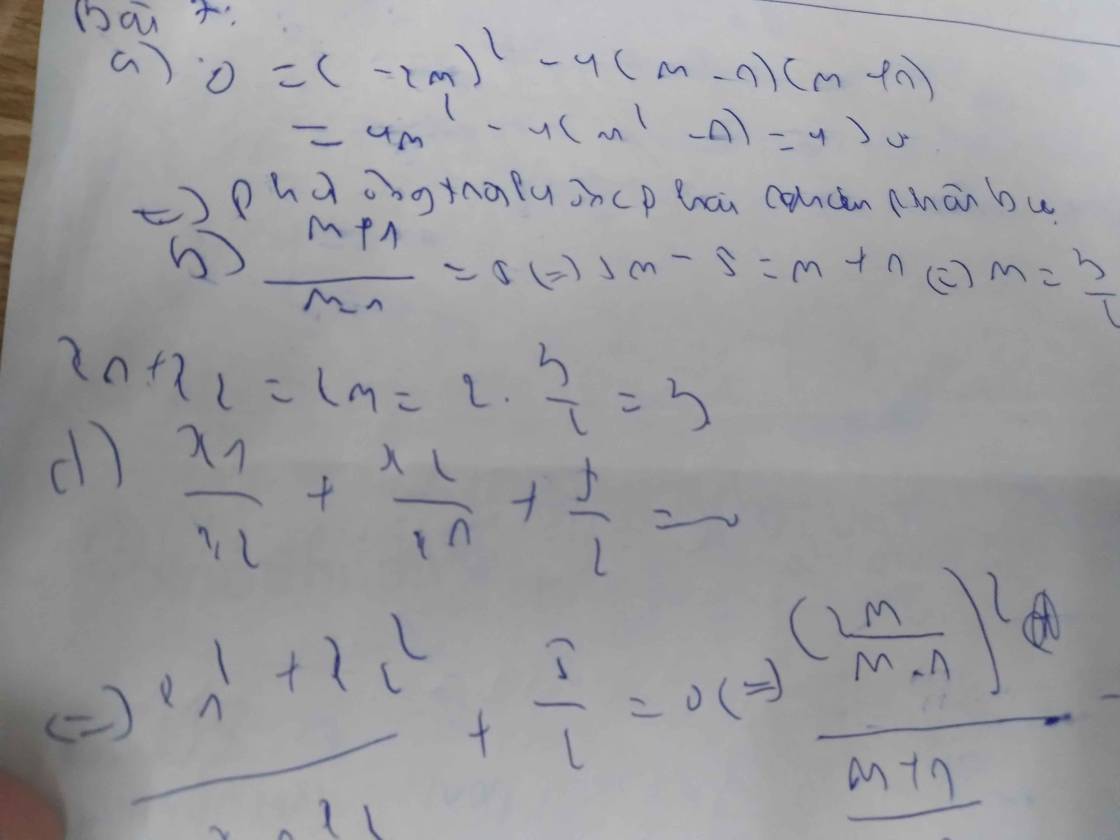Biết phương trình x^2+(m-1)x-2=0 có hai nghiệm phân biệt. Biểu diễn tổng hai nghiệm đó theo m.
H24
Những câu hỏi liên quan
Khi phương trình -x^2+2x+2m-1=0 có hai nghiệm phân biệt, hãy biểu diễn tích hai nghiệm đó theo m.
viet bình thường thôi bạn :)
Cho phương trình x^2 + 2(m - 3)x + m^2 =0 a. Giải phương trình với m = 0 b. Tìm m pt có hai nghiệm phân biệt. Tính tổng và tích hai nghiệm theo m
a. Bạn tự giải
b.
Pt có 2 nghiệm phân biệt khi:
\(\Delta'=\left(m-3\right)^2-m^2>0\)
\(\Leftrightarrow-6m+9>0\)
\(\Leftrightarrow m< \dfrac{3}{2}\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m-3\right)\\x_1x_2=m^2\end{matrix}\right.\)
Đúng 0
Bình luận (0)
a)Cho phương trình : (m+2)x^2 - (2m-1)x-3+m0 tìm điều kiện của m để phương trình có hai nghiệm phân biệt x1, x2 sao cho nghiệm này gấp đôi nghiệm kiab)Cho phương trình bậc hai: x^2-mx+m-10. Tìm m để phương trình có hai nghiệm x1;x2 sao cho biểu thức R2x1x2+3/x1^2+x2^2+2(1+x1x2) đạt giá trị lớn nhất. Tìm giá trị lớn nhất đóc)Định m để hiệu hai nghiệm của phương trình sau đây bằng 2mx^2-(m+3)x+2m+10Mọi người giúp em giải chi tiết ra với ạ. Em cảm ơn!
Đọc tiếp
a)Cho phương trình : (m+2)x^2 - (2m-1)x-3+m=0 tìm điều kiện của m để phương trình có hai nghiệm phân biệt x1, x2 sao cho nghiệm này gấp đôi nghiệm kia
b)Cho phương trình bậc hai: x^2-mx+m-1=0. Tìm m để phương trình có hai nghiệm x1;x2 sao cho biểu thức R=2x1x2+3/x1^2+x2^2+2(1+x1x2) đạt giá trị lớn nhất. Tìm giá trị lớn nhất đó
c)Định m để hiệu hai nghiệm của phương trình sau đây bằng 2
mx^2-(m+3)x+2m+1=0
Mọi người giúp em giải chi tiết ra với ạ. Em cảm ơn!
a Tìm m để phương trình x^2-left(2m+1right)x+m^2+10 có hai nghiệm phân biệt trong đó nghiệm nàygấp đôi nghiệm kiab Tìm m để phương trình x^2-2mx+m-30 có hai nghiệm x_1,x_2 thỏa mãn x_1+2x_2 1c Tìm m để phương trình x^2-2mx+left(m-1right)^30 có hai nghiệm trong đó nghiệm này là bìnhphương của nghiệm kia .d Tìm m để phương trình 2x^2-left(m+1right)x+m+30 có hai nghiệm sao cho hiệu hai nghiệm bằng 1.
Đọc tiếp
a Tìm m để phương trình \(x^2-\left(2m+1\right)x+m^2+1=0\)
có hai nghiệm phân biệt trong đó nghiệm này
gấp đôi nghiệm kia
b Tìm m để phương trình \(x^2-2mx+m-3=0\) có hai nghiệm \(x_1,x_2\) thỏa mãn \(x_1+2x_2\) =1
c Tìm m để phương trình \(x^2-2mx+\left(m-1\right)^3=0\)
có hai nghiệm trong đó nghiệm này là bình
phương của nghiệm kia .
d Tìm m để phương trình \(2x^2-\left(m+1\right)x+m+3=0\) có hai nghiệm sao cho hiệu hai nghiệm bằng 1.
d: Ta có: \(\text{Δ}=\left(m+1\right)^2-4\cdot2\cdot\left(m+3\right)\)
\(=m^2+2m+1-8m-24\)
\(=m^2-6m-23\)
\(=m^2-6m+9-32\)
\(=\left(m-3\right)^2-32\)
Để phương trình có hai nghiệm phân biệt thì \(\left(m-3\right)^2>32\)
\(\Leftrightarrow\left[{}\begin{matrix}m-3>4\sqrt{2}\\m-3< -4\sqrt{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m>4\sqrt{2}+3\\m< -4\sqrt{2}+3\end{matrix}\right.\)
Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{m+1}{2}\\x_1x_2=\dfrac{m+3}{2}\end{matrix}\right.\)
Ta có: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{m+1}{2}\\x_1-x_2=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x_1=\dfrac{m+3}{2}\\x_2=x_1-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1=\dfrac{m+3}{4}\\x_2=\dfrac{m+3}{4}-\dfrac{4}{4}=\dfrac{m-1}{4}\end{matrix}\right.\)
Ta có: \(x_1x_2=\dfrac{m+3}{2}\)
\(\Leftrightarrow\dfrac{\left(m+3\right)\left(m-1\right)}{16}=\dfrac{m+3}{2}\)
\(\Leftrightarrow\left(m+3\right)\left(m-1\right)=8\left(m+3\right)\)
\(\Leftrightarrow\left(m+3\right)\left(m-9\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=-3\\m=9\end{matrix}\right.\)
Đúng 1
Bình luận (1)
Cho phương trình: x²-2(m-3)x+(m-4)=0 (1) a) giải phương trình với m=1 b) Chứng minh phương trình (1) luôn có hai nghiệm phân biệt c) Xác định m để phương trình có hai nghiệm trái dấu d)Tính theo m giá trị của biểu thức A=1/x1+1/x2.Tìm m để A € Z để A € Z
a: Khi m=1 thì pt sẽ là: x^2+4x-3=0
=>x=-2+căn 7 hoặc x=-2-căn 7
b: Δ=(2m-6)^2-4(m-4)
=4m^2-24m+36-4m+16
=4m^2-28m+52=(2m-7)^2+3>0
=>PT luôn có hai nghiệm pb
c: PT có hai nghiệm trái dấu
=>m-4<0
=>m<4
Đúng 0
Bình luận (0)
Bài 7: Cho phương trình (m - 1) * x ^ 2 - 2mx + m + 1 0 với m là thamsốa) CMR phương trình luôn có hai nghiệm phân biệt Vm#1 b) Xác định giá trị của m để phương trình có tích hai nghiệm bằng 5, từ đó hãy tính tổng hai nghiêm của phương trìnhc) Tìm một hệ thức liên hệ giữa hai nghiệm không phụ thuộc vào md) Tìm m để phương trình có nghiệm Xi; xz thoả mãn hệ thức: x1/x2+x2/x1+5/20
Đọc tiếp
Bài 7: Cho phương trình (m - 1) * x ^ 2 - 2mx + m + 1 = 0 với m là tham
số
a) CMR phương trình luôn có hai nghiệm phân biệt Vm#1 b) Xác định giá trị của m để phương trình có tích hai nghiệm bằng 5, từ đó hãy tính tổng hai nghiêm của phương trình
c) Tìm một hệ thức liên hệ giữa hai nghiệm không phụ thuộc vào m
d) Tìm m để phương trình có nghiệm Xi; xz thoả mãn hệ thức: x1/x2+x2/x1+5/2=0
tìm m để phương trình x^2+2(m+2)x+m+7=0 có hai nghiệm phân biệt và tổng bình phương của hai nghiệm bằng 14m+6
CÂU 13: PT BẬC HAI – HỆ THỨC VIET
Cho phương trình bậc hai : x ^ 2 - 2(m - 2) * x + m ^ 2 - 3 0 với m là
tham số.
1) Tìm m để phương trình có hai nghiệm phân biệt x_{1}; x_{2} .
2) Tìm m để phương trình có hai nghiệm phân biệt x_{1} / x_{2} thỏa: x_{1} ^ 2 + x_{2} ^ 2 22
3) Tìm m để phương trình có hai nghiệm X_{1} ; X_{2} thỏa: A x_{1} ^ 2 + x_{2} ^ 2 + 2021 đạt giá trị nhỏ nhất và tim giá trị nhỏ nhất đó
Đọc tiếp
CÂU 13: PT BẬC HAI – HỆ THỨC VIET Cho phương trình bậc hai : x ^ 2 - 2(m - 2) * x + m ^ 2 - 3 = 0 với m là tham số. 1) Tìm m để phương trình có hai nghiệm phân biệt x_{1}; x_{2} . 2) Tìm m để phương trình có hai nghiệm phân biệt x_{1} / x_{2} thỏa: x_{1} ^ 2 + x_{2} ^ 2 = 22 3) Tìm m để phương trình có hai nghiệm X_{1} ; X_{2} thỏa: A = x_{1} ^ 2 + x_{2} ^ 2 + 2021 đạt giá trị nhỏ nhất và tim giá trị nhỏ nhất đó
1:
Δ=(2m-4)^2-4(m^2-3)
=4m^2-16m+16-4m^2+12=-16m+28
Để PT có hai nghiệm phân biệt thì -16m+28>0
=>-16m>-28
=>m<7/4
2: x1^2+x2^2=22
=>(x1+x2)^2-2x1x2=22
=>(2m-4)^2-2(m^2-3)=22
=>4m^2-16m+16-2m^2+6=22
=>2m^2-16m+22=22
=>2m^2-16m=0
=>m=0(nhận) hoặc m=8(loại)
3: A=x1^2+x2^2+2021
=2m^2-16m+2043
=2(m^2-8m+16)+2011
=2(m-4)^2+2011>=2011
Dấu = xảy ra khi m=4
Đúng 0
Bình luận (0)
Cho phương trình x² +(m+3)x-2m+2=0 a. Tìm m để phương trình có hai nghiệm trái dấu. b. Tìm m để phương trình có hai nghiệm dương phân biệt. c. Tìm m để phương trình có hai nghiệm âm phân biệt. d. Tìm m để phương trình có ít một nghiệm dương.
Sửa đề: \(x^2+\left(m+3\right)x+2m+2=0\)
a: Để phương trình có hai nghiệm trái dấu thì 2m+2<0
hay m<-1
b: \(\text{Δ}=\left(m+3\right)^2-4\left(2m+2\right)\)
\(=m^2+6m+9-8m-8\)
\(=m^2-2m+1=\left(m-1\right)^2>=0\)
Do đó: Phương trình luôn có hai nghiệm với mọi m
Để phương trình có hai nghiệm dương phân biệt thì \(\left\{{}\begin{matrix}m-1< >0\\2m+2>0\\m+3>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>-1\\m< >1\end{matrix}\right.\)
Đúng 0
Bình luận (0)