Trong mặt phẳng Oxy, cho tam giác ABC có A(2;3),I(6;6),J(4;5) lần lượt là tâm đường tròn ngoại tiếp và nội tiếp của tam giác ABC. Tìm phương trình đường thẳng BC
LH
Những câu hỏi liên quan
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 1, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích V của khối cầu ngoại tiếp hình chóp đã cho. A.
5
π
15
18
B.
5
π
15
54...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 1, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích V của khối cầu ngoại tiếp hình chóp đã cho.
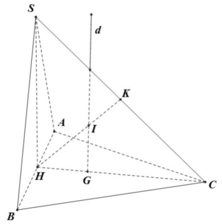
A. 5 π 15 18
B. 5 π 15 54
C. 4 π 3 27
D. 5 π 3
Cho tam giác ABC có góc B = 90 độ, BH là đường cao. Gọi M trung điểm HC, G là trực tâm của tam giác ABM. Kẻ Ax // BC, trên đường đó lấy P có AP = 1/2 BC và nằm ở nửa mặt phẳng đối của nửa mặt phẳng chứa B có bờ AC. a/ Hỏi AGMP là hình gì? b/Chứng minh tam giác AGM đồng dạng với tam giác MPA c/ tính góc PMB
Giải nhanh giúp mình nhé!
trong mặt phẳng tọa đọ Oxy cho A(1,2); B(-2,1) a) Tính diện tích tam giác OAB và tọa độ giao điểm M của AB với trục hoành b) Tìm tọa độ tâm đường tròn ngoại tiếp tam giác ABC?
trong mặt phẳng oxy cho tam giác ABC A(2;4) B(-6;0) C(2;0) tìm K sao cho K thuộc Oy và KA + KB +KC nhỏ nhất
Cho tam giác ABC có góc A khác 60 độ.Ở phía ngoài tam giác ABC vẽ các tam giác đều tam giác ABD và tam giác ACE.Trên nửa mặt phẳng bờ BC có chứa điểm A vẽ tam giác BCK.CMR: ADKE là hình bình hành
Một khung ABC có dạng một tam giác đều, có cạnh bằng ℓ, nằm trong mặt phẳng nằm ngang. Tác dụng một lực có độ lớn F nằm trong mặt phẳng nằm ngang và song song với cạnh BC, vào điểm A của khung. Momen của lực đối với trục quay đi qua C và vuông góc với mặt phẳng khung là A. F.ℓ. B. F.ℓ/2. C.
F
l
3
D.
F
l
3
2
Đọc tiếp
Một khung ABC có dạng một tam giác đều, có cạnh bằng ℓ, nằm trong mặt phẳng nằm ngang. Tác dụng một lực có độ lớn F nằm trong mặt phẳng nằm ngang và song song với cạnh BC, vào điểm A của khung. Momen của lực đối với trục quay đi qua C và vuông góc với mặt phẳng khung là
A. F.ℓ.
B. F.ℓ/2.
C. F l 3
D. F l 3 2
Chọn D.
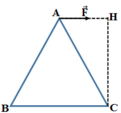
Cánh tay đòn của lực F → là CH. Do đó momen của lực F → đối với trục quay đi qua C và vuông góc với mặt phẳng khung là: MF/C = F.CH = Fℓ 3 /2.
Đúng 0
Bình luận (0)
Một khung ABC có dạng một tam giác đều, có cạnh bằng ℓ, nằm trong mặt phẳng nằm ngang. Tác dụng một lực có độ lớn F nằm trong mặt phẳng nằm ngang và song song với cạnh BC, vào điểm A của khung. Momen của lực F đối với trục quay đi qua C và vuông góc với mặt phẳng khung là A.
F
.
l
B.
F
.
l
/
2
C.
F
.
l
3
D. ...
Đọc tiếp
Một khung ABC có dạng một tam giác đều, có cạnh bằng ℓ, nằm trong mặt phẳng nằm ngang. Tác dụng một lực có độ lớn F nằm trong mặt phẳng nằm ngang và song song với cạnh BC, vào điểm A của khung. Momen của lực F đối với trục quay đi qua C và vuông góc với mặt phẳng khung là
A. F . l
B. F . l / 2
C. F . l 3
D. F . l 3 / 2
Chọn D.
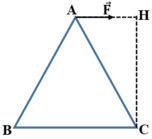
Cánh tay đòn của lực F ⇀ là CH. Do đó momen của lực F→ đối với trục quay đi qua C và vuông góc với mặt phẳng khung là:
M F / C = F.CH = F . l 3 / 2
Đúng 0
Bình luận (0)
trong mặt phẳng tọa độ Oxy cho A(-3;6); B(1;-2); C(6;3) a) Tìm tọa độ tâm đường tròn ngoại tiếp tam giác ABC?b) Tìm toạ độ tâm K đường tròn nội tiếpc) Tìm toạ độ H là trực tâm của tam giác đó d) Tìm toạ độ điểm E với E là đường cao kẻ từ Ae) Tìm toạ độ điểm G với G là chân đường phân giác kẻ từ A xuống BCGiúp em vs , bài hơi khó
Đọc tiếp
trong mặt phẳng tọa độ Oxy cho A(-3;6); B(1;-2); C(6;3)
a) Tìm tọa độ tâm đường tròn ngoại tiếp tam giác ABC?
b) Tìm toạ độ tâm K đường tròn nội tiếp
c) Tìm toạ độ H là trực tâm của tam giác đó
d) Tìm toạ độ điểm E với E là đường cao kẻ từ A
e) Tìm toạ độ điểm G với G là chân đường phân giác kẻ từ A xuống BC
Giúp em vs , bài hơi khó
a, Gọi \(I\left(x;y\right)\) là tâm đường tròn ngoại tiếp \(\Delta ABC\)
\(\Rightarrow\left\{{}\begin{matrix}IA=IB\\IA=IC\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}IA^2=IB^2\\IA^2=IC^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(-3-x\right)^2+\left(6-y\right)^2=\left(1-x\right)^2+\left(-2-y\right)^2\\\left(-3-x\right)^2+\left(6-y\right)^2=\left(6-x\right)^2+\left(3-y\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-2y=-5\\3x-y=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=3\end{matrix}\right.\)
Đúng 2
Bình luận (1)
Cho tam giác ABC. Trên nửa mặt phẳng bờ BC không chứa điểm A, vẽ tia Bx; trên nửa mặt phẳng bờ BC có chứa điểm A, vẽ tia Cy sao cho
Trên Bx, Cy lần lượt lấy hai điểm D và E sao cho .
Gọi G là trọng tâm của tam giác ABC.
Chứng minh rằng G cũng là trọng tâm của tam giác ADE



