Chọn A.

Gọi AH là đường cao của tam giác ABC ⇒ AH ⊥ BC.

B(4;5), C(-3;2)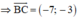 

Phương trình đường cao AH đi qua A(2;-1) nhận 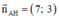 là VTPT là:

7.(x - 2) + 3.(y + 1) = 0 ⇔ 7x - 14 + 3y + 3 = 0 ⇔ 7x + 3y - 11 = 0

Vậy phương trình đường cao AH là 7x + 3y - 11 = 0.

\(\overrightarrow{AB}=\left(4;-3\right)\Rightarrow AB=5\)

\(\overrightarrow{AC}=\left(6;0\right)\Rightarrow AC=6\)

\(\overrightarrow{BC}=\left(2;3\right)\Rightarrow BC=\sqrt{13}\)

Chu vi tam giác: \(AB+AC+BC=11+\sqrt{13}\)

vecto AH=(x+2;y-4); vecto BC=(-6;-2)

vecto BH=(x-4;y-1); vecto AC=(0;-5)

Theo đề, ta có: -6(x+2)-2(y-4)=0 và 0(x-4)-5(y-1)=0

=>y=1 và -6(x+2)=2(y-4)=2*(1-4)=-6

=>x+2=1 và y=1

=>x=-1 và y=1

\(AB=\sqrt{\left(0+1\right)^2+\left(2+3\right)^2}=\sqrt{26}\)

\(AC=\sqrt{\left(2+1\right)^2+\left(1+3\right)^2}=\sqrt{3^2+4^2}=5\)

\(BC=\sqrt{\left(2-0\right)^2+\left(1-2\right)^2}=\sqrt{5}\)

=>\(C=\sqrt{26}+5+\sqrt{5}\left(cm\right)\)

\(AB=\sqrt{\left(5-1\right)^2+\left(-3+1\right)^2}=2\sqrt{5}\)

\(AC=\sqrt{\left(0-1\right)^2+\left(1+1\right)^2}=\sqrt{5}\)

\(BC=\sqrt{\left(0-5\right)^2+\left(1+3\right)^2}=\sqrt{29}\)

=>C=3 căn 5+căn 29

\(\overrightarrow{AB}=\left(1;-2\right)\Rightarrow AB=\sqrt{5}\)

\(\overrightarrow{AC}=\left(-2;2\right)\Rightarrow AC=2\sqrt{2}\)

\(BC=\left(-3;4\right)\Rightarrow BC=5\)

Chu vi tam giác ABC: \(AB+AC+BC=\sqrt{5}+2\sqrt{2}+5\)

\(\left\{{}\begin{matrix}\overrightarrow{AB}=\left(-1;-2\right)\\\overrightarrow{AC}=\left(4;-2\right)\end{matrix}\right.\)

\(\Rightarrow\overrightarrow{AB}.\overrightarrow{AC}=-1.4+\left(-2\right).\left(-2\right)=0\)

\(\Rightarrow\Delta ABC\) vuông tại A

\(\overrightarrow{AB}\left(2;2\right);\overrightarrow{AC}\left(2;-2\right)\)
\(\overrightarrow{AB}.\overrightarrow{AC}=2.2+2.\left(-2\right)=0\) nên \(AB\perp AC\). (1)
\(AB=\sqrt{2^2+2^2}=2\sqrt{2}\).
\(AC=\sqrt{2^2+\left(-2\right)^2}=2\sqrt{2}\)
Vì vậy AB = AC. (2)
Từ (1) và (2) suy ra tam giác ABC vuông cân tại A.