M=
Với a>0;a≠1
\(\left(\frac{1}{1-\sqrt{a}}-\frac{1}{1+\sqrt{a}}\right)×\left(\frac{1}{\sqrt{a}}-1\right)\)
Trong không gian với hệ tọa độ Oxy, cho hình hộp chữ nhật ABCD.A'B'C'D' có A trùng với gốc tọa độ O, các đỉnh B(m; 0; 0), D(0; m; 0), A'(0; 0;n) với m, n>0 và m+n=4. Gọi M là trung điểm của cạnh CC'. Khi đó thể tích tứ diện BDA'M đạt giá trị lớn nhất bằng:
A. 245 108
B. 9 4
C. 64 27
D. 75 32
Trong không gian với hệ tọa độ Oxyz, cho hình hộp chữ nhật ABCD.A’B’C’D’ có A trùng với gốc tọa độ O, các đỉnh B (m; 0; 0), D (0; m; 0), A’ (0; 0; n) với m, n > 0 và m + n = 4. Gọi M là trung điểm của cạnh CC’. Khi đó thể tích tứ diện BDA’M đạt giá trị lớn nhất bằng:
A. 245/108
B. 9/4
C. 64/27
D. 75/32
Chọn C
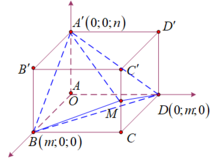
Ta chia khối hộp chữ nhật ABCD.A’B’C’D’ thành các hình chóp có thể tích:
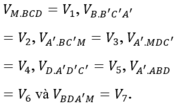
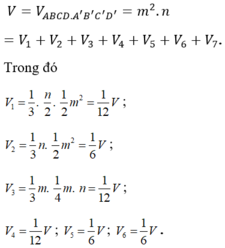
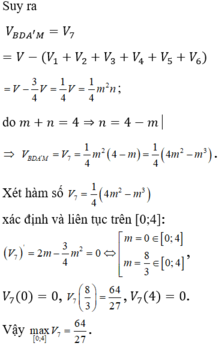
Cho m = a.b.c^2 với a,b,a,b,c € z .biết m<0 ,a>0 ,c<0 . hãy so sánh b với số 0
cho M=\(\left(\dfrac{1}{a-\sqrt{a}}+\dfrac{1}{\sqrt{a}-1}\right).\dfrac{\sqrt{a}+1}{a-2\sqrt{a}+1}\) với 0<a\(\ne\)1
a.rút gọn M
b.so sanh M với 1
c.tìm a để M>0
\(a,Sửa:M=\left(\dfrac{1}{a-\sqrt{a}}+\dfrac{1}{\sqrt{a}-1}\right):\dfrac{\sqrt{a}+1}{a-2\sqrt{a}+1}\\ M=\dfrac{\sqrt{a}+1}{\sqrt{a}\left(\sqrt{a}-1\right)}\cdot\dfrac{\left(\sqrt{a}-1\right)^2}{\sqrt{a}+1}=\dfrac{\sqrt{a}-1}{\sqrt{a}}\\ b,M=\dfrac{\sqrt{a}-1}{\sqrt{a}}=1-\dfrac{1}{\sqrt{a}}< 1\left(\dfrac{1}{\sqrt{a}}>0\right)\\ c,M>0\Leftrightarrow\sqrt{a}-1>0\left(\sqrt{a}>0\right)\Leftrightarrow a>1\)
trong măt phang Oxy cho 3 điểm A(0;a), B(b;0) Và C(-b;0) với a>0 b>0. Tìm toa độ tâm I của đưong tròn tiếp xúc với AB tai B Và tiếp xúc với AC tại C
\(AB=AC=\sqrt{a^2+b^2}\) (1)
Do (C) tiếp xúc AB tại B và AC tại C \(\Rightarrow IA=IB=R\) (2)
Từ (1) và (2) \(\Rightarrow IA\) là trung trực của BC
Mà B và C nằm trên Ox, A nằm trên Oy \(\Rightarrow I\) nằm trên Oy \(\Rightarrow I\left(0;y\right)\)
\(\Rightarrow IA=y_A-y_I=a-y\)
Theo hệ thức lượng ta có:
\(IA.OA=AB^2\Leftrightarrow IA=\frac{AB^2}{OA}\Leftrightarrow a-y=\frac{a^2+b^2}{a}\)
\(\Rightarrow y=a-\frac{a^2+b^2}{a}=\frac{-b^2}{a}\Rightarrow I\left(0;-\frac{b^2}{a}\right)\)
Phân tích các đa thức sau thành nhân tử :
a) a+b ( với a > 0 và b < 0 )
b) 5 - 2a ( với a > 0 )
c) a - 6 căn bậc a ( với a> 0 )
d) ( căn bậc a ) ^3 - 3a +3 căn bậc a -1 ( với a > 0)
Mọi người giúp mình với ạ , mình sắp nộp rồi cảm ơn nhiều ạ !!!!!!!!!!!!
Trả lời:
a/ \(a+b=a-\left(-b\right)=\left(\sqrt{a}\right)^2-\left(\sqrt{b}\right)^2=\left(\sqrt{a}+\sqrt{b}\right).\left(\sqrt{a}-\sqrt{b}\right)\)
b/ \(5-2a=\left(\sqrt{5}\right)^2-\left(\sqrt{2a}\right)^2=\left(\sqrt{5}-\sqrt{2a}\right).\left(\sqrt{5}+\sqrt{2a}\right)\)
c/ \(a-6\sqrt{a}=\left(\sqrt{a}\right)^2-6\sqrt{a}=\sqrt{a}.\left(\sqrt{a}-6\right)\)
d/ \(\left(\sqrt{a}\right)^3-3a+3\sqrt{a}-1=\left(\sqrt{a}\right)^3-3\left(\sqrt{a}\right)^2+3\sqrt{a}-1=\left(\sqrt{a}-1\right)^3\)
Cho phân số a/b (a, b ∈ N, b # 0)
Giả sử a/b<1 và m ∈ N, m ≠ 0. Chứng tỏ rằng:
a/b<a+m/b+m
giúp mình với![]()
![]()
![]()
Cho PT ax^8 + bx^5 + c = 0. Với a + b + mc = 0 m thuộc R. CMR PT luôn có nghiệm với m>1
Cho PT ax^8 + bx^5 + c = 0. Với a + b + mc = 0 m thuộc R. CMR PT luôn có nghiệm với m>1
cho a,b,m khác 0 thỏa mãn a+b+m=0 tính (1+a/b)×(1+b/m)×(1+m/a) Xin mn giúp mik với ạ mik sắp thi rùi😓😓😓
a+b=-m; b+m=-a; a+m=-b
A=(a+b)/b*(m+b)/m*(m+a)/a=-1