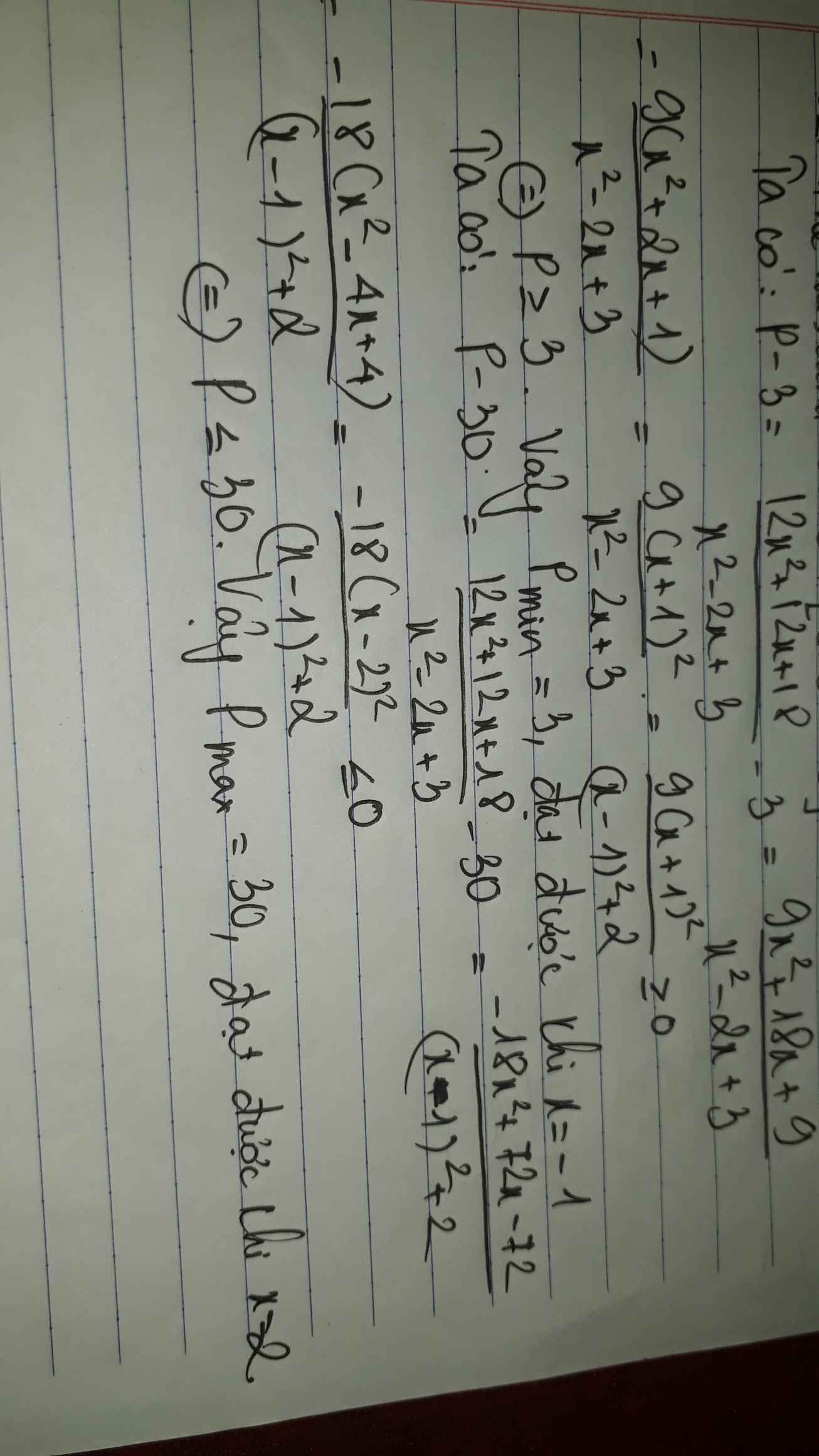Tìm giá trị nhỏ nhất : 2^2 + 12x +19
SN
Những câu hỏi liên quan
a, Tìm giá trị lớn nhất của biểu thức: A=4x-x^2+3
b. Tìm giá trị nhỏ nhất của biểu thức:B=4x^2-12x+15
c,Tìm giá trị nhỏ nhất của biểu thức:C=4x^2+2y^2-4xy-4y+1
a)
\(A=4x-x^2+3=-\left(x^2-4x-3\right)=-\left(x^2-4x+4\right)+7=-\left(x-2\right)^2+7\le7\)
Daaus = xayr ra khi: x = 2
b) \(B=4x^2-12x+15=4\left(x^2-3x+9\right)-21=4\left(x-3\right)^2-21\ge-21\)
Dấu = xảy ra khi x = 3
c) \(C=4x^2+2y^2-4xy-4y+1=\left(4x^2-4xy+y^2\right)+\left(y^2-4y+4\right)-3=\left(2x-y\right)^2+\left(y-2\right)^2-3\ge-3\)
Dấu = xảy ra khi
2x = y và y = 2
=> x = 1 và y = 2
Đúng 1
Bình luận (0)
a) A = \(-x^2+4x+3=-\left(x-2\right)^2+7\le7\)
Dấu "=" <=> x = 2
b) \(4x^2-12x+15=\left(2x-3\right)^2+6\ge6\)
Dấu "=" xảy ra <=> \(x=\dfrac{3}{2}\)
c) \(4x^2+2y^2-4xy-4y+1\)
= \(\left(4x^2-4xy+y^2\right)+\left(y^2-4y+4\right)-3\)
= \(\left(2x-y\right)^2+\left(y-2\right)^2-3\ge-3\)
Dấu "=" <=> \(\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Tìm giá trị lớn nhất, nhỏ nhất của biểu thức:
\(P=\dfrac{12x^2+12x+18}{x^2-2x+3}\)
Tìm giá trị nhỏ nhất và giá trị lớn nhất của:
A = \(\dfrac{27-12x}{x^2+9}\)
\(A=\dfrac{27-12x}{x^2+9}=\dfrac{x^2-12x+36-\left(x^2+9\right)}{x^2+9}=\dfrac{\left(x-6\right)^2}{x^2+9}-1\ge-1\)
\(A_{min}=-1\Leftrightarrow x=6\)
\(A=\dfrac{27-12x}{x^2+9}=\dfrac{4\left(x^2+9\right)-\left(4x^2+12x+9\right)}{x^2+9}=4-\dfrac{\left(2x+3\right)^2}{x^2+9}\le4\)
\(A_{max}=4\Leftrightarrow x=\dfrac{-3}{2}\)
Đúng 1
Bình luận (0)
Tìm giá trị nhỏ nhất: 9x^2-12x
Tìm giá trị nhỏ nhất của :
A=x^2 - 12x + 6y^2 -2xy + 2y +150
Xem chi tiết
\(A=\left(x^2+y^2+36-2xy-12x+12y\right)+5y^2-10y+5+109\)
\(A=\left(x-y-6\right)^2+5\left(y-1\right)^2+109\ge109\)
\(A_{min}=109\) khi \(\left\{{}\begin{matrix}x=7\\y=1\end{matrix}\right.\)
Đúng 0
Bình luận (0)
tìm giá trị lớn nhất nhỏ nhất của Q=(12x+16)/(x^2+1)
Tìm giá trị lớn nhất và nhỏ nhất của: \(C=\dfrac{27-12x}{x^2+9}\)
\(C=\dfrac{4\left(x^2+9\right)-4x^2-12x-9}{x^2+9}=4-\dfrac{\left(2x+3\right)^2}{x^2+9}\le4\)
\(C_{max}=9\) khi \(x=-\dfrac{3}{2}\)
\(C=\dfrac{-x^2-9+x^2-12x+36}{x^2+9}=-1+\dfrac{\left(x-6\right)^2}{x^2+9}\ge-1\)
\(C_{min}=-1\) khi \(x=6\)
Đúng 2
Bình luận (0)
Ta có \(4-C=\dfrac{4x^2+12x+9}{x^2+3}=\dfrac{\left(2x+3\right)^2}{x^2+3}\ge0\Rightarrow C\le4\).
Đẳng thức xảy ra khi và chỉ khi \(x=-\dfrac{3}{2}\).
\(C+1=\dfrac{x^2-12x+36}{x^2+9}=\dfrac{\left(x-6\right)^2}{x^2+9}\ge0\Rightarrow C\ge-1\).
Đẳng thức xảy ra khi và chỉ khi x = 6.
Đúng 2
Bình luận (0)
Tìm giá trị nhỏ nhất:
A= x^2 - 12x + 18
\(A=x^2-12x+18\)
\(A=x^2-2.x.6+36-36+18\)
\(A=\left(x-6\right)^2-18\)
Vì \(\left(x-6\right)^2\ge0\)
Nên \(\left(x-6\right)^2-18\ge-18\)
Vậy \(A_{MIN}=-18\Leftrightarrow x-6=0\Leftrightarrow x=6\)
Đúng 0
Bình luận (0)
Ta có : \(A=x^2-12x+18\)
\(=x^2-2.x.6+6^2-18\)
\(=\left(x-6\right)^2-18\)
Có : \(\left(x-6\right)^2\ge0\)
\(\Rightarrow\left(x-6\right)^2-18\ge-18\)
Dấu " = " xảy ra khi \(x-6=0\)
\(x=6\)
Vậy \(MIN_A=-18\) khi \(x=6\)
Đúng 0
Bình luận (0)
A= x2 - 12x + 18
=x2 - 12x + 36-18
=(x-6)2-18\(\ge\)-18
Dấu = khi x=6
Vậy MinA=-18 khi x=6
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tìm giá trị nhỏ nhất của biểu thức:
B= \(\dfrac{2x^{2^{ }}-12x+25}{x^{2^{ }}-6x+12}\)
\(B=\dfrac{2x^2-12x+25}{x^2-6x+12}=\dfrac{2\left(x^2-6x+12\right)+1}{x^2-6x+12}=2+\dfrac{1}{x^2-6x+9+4}=2+\dfrac{1}{\left(x-3\right)^2+4}\le2+\dfrac{1}{4}=\dfrac{9}{4}\)
Không có min nha bạn . Chỉ có max thôi
Dấu = xảy ra khi x=3
Đúng 2
Bình luận (0)
tìm giá trị nhỏ nhất 9x2 -12x+10
pt\(\Leftrightarrow9x^2-12x+4+6=\left(3x-2\right)^2+6\ge6\)
dấu = xảy ra khi \(x=\frac{2}{3}\)
(nhớ k nhé)
Đúng 0
Bình luận (0)