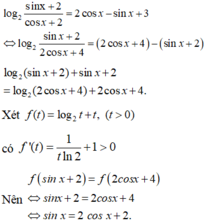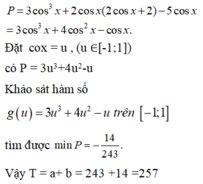tìm giá trị biểu thức \(B=sinx+5cosx/sin^3x-2cos^3x\) biết tanx=2
NN
Những câu hỏi liên quan
Biết \(sinx+cosx=m\).
Tính giá trị biểu thức sau theo m: \(sin^3x+cos^3x\)
sin x+cosx=m
=>(sinx+cosx)^2=m^2
=>1+2*cosx*sinx=m^2
=>2*sinx*cosx=m^2-1
=>\(sinx\cdot cosx=\dfrac{m^2-1}{2}\)
\(sin^3x+cos^3x=\left(sinx+cosx\right)^3-3\cdot sinx\cdot cosx\cdot\left(sinx+cosx\right)\)\(=m^3-3\cdot\dfrac{m^2-1}{2}\cdot m\)
\(=m^3-\dfrac{3m^3-3m}{2}\)
\(=\dfrac{2m^3-3m^3+3m}{2}=\dfrac{-m^3+3m}{2}\)
Đúng 0
Bình luận (0)
Cho các số thực x,y thay đổi thỏa mãn
log
2
sin
x
+
2
cos
x
+
2
2
cos
x
-
sin
x...
Đọc tiếp
Cho các số thực x,y thay đổi thỏa mãn log 2 sin x + 2 cos x + 2 = 2 cos x - sin x + 3 . Gọi - a b với a , b ∈ ℕ * , a b tối giản là giá trị nhỏ nhất của biểu thức P = 3 cos 3 x + sin 2 x - 5 cos x Tính T = a +b
A. T = 200
B. T = 257
C. T = 210
D. T = 240
Cho tanx=5. Tính
\(A=\frac{3sinx-4cosx}{cosx+2sinx}\)
\(B=\frac{sinx+sin^3x}{2cos^3x+cosx}\)
\(A=\frac{3sinx-4cosx}{cosx+2sinx}=\frac{\frac{3sinx}{cosx}-4}{1+\frac{2sinx}{cosx}}=\frac{3tanx-4}{1+2tanx}=\frac{3.5-4}{1+2.5}=...\)
\(B=\frac{\frac{sinx}{cos^3x}+\frac{sin^3x}{cos^3x}}{\frac{3cos^3x}{cos^3x}+\frac{cosx}{cos^3x}}=\frac{tanx.\frac{1}{cos^2x}+tan^3x}{3+\frac{1}{cos^2x}}=\frac{tanx\left(1+tan^2x\right)+tan^3x}{3+\left(1+tan^2x\right)}=\frac{5\left(1+5^2\right)+5^3}{3+1+5^2}=...\)
Đúng 0
Bình luận (0)
Biết \(sinx=\dfrac{-2\sqrt{5}}{5},cosx=\dfrac{1}{\sqrt{5}},tanx=-2\). Tính giá trị của biểu thức: M = \(sin\left(\dfrac{\pi}{2}-x\right).cot\left(\pi+x\right)\)
\(sin(\dfrac{\pi}{2}-x)cot(\pi+x)=cosxcotx=\dfrac{cosx}{tanx}\\ =\dfrac{\dfrac{1}{\sqrt5}}{-2}=\dfrac{-\sqrt5}{10}\)
Đúng 0
Bình luận (0)
1,Giải phương trình:
a,\(cos^3x+sin^3x=cos2x\)
b,\(cos^3x+sin^3x=2sin2x+sinx+cosx\)
c,\(2cos^3x=sin3x\)
d,\(cos^2x-\sqrt{3}sin2x=1+sin^2x\)
e,\(cos^3x+sin^3x=2\left(cos^5x+sin^5x\right)\)
a, (sinx + cosx)(1 - sinx . cosx) = (cosx - sinx)(cosx + sinx)
⇔ \(\left[{}\begin{matrix}sinx+cosx=0\\cosx-sinx=1-sinx.cosx\end{matrix}\right.\)
⇔ \(\left[{}\begin{matrix}sinx+cosx=0\\cosx+sinx.cosx-1-sinx=0\end{matrix}\right.\)
⇔ \(\left[{}\begin{matrix}sinx+cosx=0\\\left(cosx-1\right)\left(sinx+1\right)=0\end{matrix}\right.\)
⇔ \(\left[{}\begin{matrix}sin\left(x+\dfrac{\pi}{4}\right)=0\\cosx=1\\sinx=-1\end{matrix}\right.\)
b, (sinx + cosx)(1 - sinx . cosx) = 2sin2x + sinx + cosx
⇔ (sinx + cosx)(1 - sinx.cosx - 1) = 2sin2x
⇔ (sinx + cosx).(- sinx . cosx) = 2sin2x
⇔ 4sin2x + (sinx + cosx) . sin2x = 0
⇔ \(\left[{}\begin{matrix}sin2x=0\\\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)+4=0\end{matrix}\right.\)
⇔ sin2x = 0
c, 2cos3x = sin3x
⇔ 2cos3x = 3sinx - 4sin3x
⇔ 4sin3x + 2cos3x - 3sinx(sin2x + cos2x) = 0
⇔ sin3x + 2cos3x - 3sinx.cos2x = 0
Xét cosx = 0 : thay vào phương trình ta được sinx = 0. Không có cung x nào có cả cos và sin = 0 nên cosx = 0 không thỏa mãn phương trình
Xét cosx ≠ 0 chia cả 2 vế cho cos3x ta được :
tan3x + 2 - 3tanx = 0
⇔ \(\left[{}\begin{matrix}tanx=1\\tanx=-2\end{matrix}\right.\)
d, cos2x - \(\sqrt{3}sin2x\) = 1 + sin2x
⇔ cos2x - sin2x - \(\sqrt{3}sin2x\) = 1
⇔ cos2x - \(\sqrt{3}sin2x\) = 1
⇔ \(2cos\left(2x+\dfrac{\pi}{3}\right)=1\)
⇔ \(cos\left(2x+\dfrac{\pi}{3}\right)=\dfrac{1}{2}=cos\dfrac{\pi}{3}\)
e, cos3x + sin3x = 2cos5x + 2sin5x
⇔ cos3x (1 - 2cos2x) + sin3x (1 - 2sin2x) = 0
⇔ cos3x . (- cos2x) + sin3x . cos2x = 0
⇔ \(\left[{}\begin{matrix}sin^3x=cos^3x\\cos2x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}sinx=cosx\\cos2x=0\end{matrix}\right.\)
⇔ \(\left[{}\begin{matrix}sin\left(x-\dfrac{\pi}{4}\right)=0\\cos2x=0\end{matrix}\right.\)
Đúng 1
Bình luận (0)
B=\(\frac{sinx+cox^2-\sqrt{3.01}tanx}{sinx\left(2x\right).cot\left(3x\right)}\)biết sin(5x)=0,29
giải các pt
a) \(\left(1+tanx\right)sin^2x=3sinx\left(cosx-sinx\right)+3\)
b) \(6sinx-2cos^3x=\frac{5sin4x.sinx}{2cos2x}\)
c) \(cos^3x=2sinx.sin\left(\frac{\pi}{3}-x\right).sin\left(x+\frac{\pi}{3}\right)\)
d) \(cos2x\left(sinx+cosx\right)-4cos^3x\left(1+sin2x\right)=0\)
a.
ĐKXĐ: \(cosx\ne0\)
Chia 2 vế cho \(cos^2x\) ta được:
\(\left(1+tanx\right).tan^2x=3tanx\left(1-tanx\right)+\frac{3}{cos^2x}\)
\(\Leftrightarrow tan^2x\left(tanx+1\right)=3tanx-3tan^2x+3+3tan^2x\)
\(\Leftrightarrow tan^2x\left(tanx+1\right)-3\left(tanx+1\right)=0\)
\(\Leftrightarrow\left(tan^2x-3\right)\left(tanx+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}tanx=1\\tanx=\sqrt{3}\\tanx=-\sqrt{3}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{4}+k\pi\\x=\frac{\pi}{3}+k\pi\\x=-\frac{\pi}{3}+k\pi\end{matrix}\right.\)
Đúng 0
Bình luận (0)
c/
\(\Leftrightarrow cos^3x=sinx\left(cos\frac{2\pi}{3}+cos2x\right)\)
\(\Leftrightarrow cos^3x=sinx\left(cos2x-\frac{1}{2}\right)\)
\(\Leftrightarrow cos^3x=2sinx\left(1-2sin^2x-\frac{1}{2}\right)\)
\(\Leftrightarrow cos^3x=sinx\left(\frac{1}{2}-2sin^2x\right)\)
\(\Leftrightarrow2cos^3x=sinx-4sin^3x\)
Nhận thấy \(cosx=0\) ko phải nghiệm, chia 2 vế cho \(cos^3x\)
\(\Leftrightarrow2=tanx\left(1+tan^2x\right)-4tan^3x\)
\(\Leftrightarrow3tan^3x-tanx+2=0\)
\(\Leftrightarrow\left(tanx+1\right)\left(3tan^2x-3tanx+2\right)=0\)
\(\Leftrightarrow tanx=-1\Rightarrow x=-\frac{\pi}{4}+k\pi\)
Đúng 0
Bình luận (0)
d/
\(\Leftrightarrow\left(cos^2x-sin^2x\right)\left(sinx+cosx\right)-4cos^3x\left(sin^2x+cos^2x+2sinx.cosx\right)=0\)
\(\Leftrightarrow\left(cosx-sinx\right)\left(sinx+cosx\right)^2-4cos^3x\left(sinx+cosx\right)^2=0\)
\(\Leftrightarrow\left(cosx-sinx-4cos^3x\right)\left(sinx+cosx\right)^2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx+cosx=0\left(1\right)\\cosx-sinx-4cos^3x=0\left(2\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow sin\left(x+\frac{\pi}{4}\right)=0\Leftrightarrow x+\frac{\pi}{4}=k\pi\)
\(\Rightarrow x=-\frac{\pi}{4}+k\pi\)
Xét \(\left(2\right)\), nhận thấy \(cosx=0\) ko phải nghiệm, chia 2 vế cho \(cos^3x\)
\(\Leftrightarrow\frac{1}{cos^2x}-tanx.\frac{1}{cos^2x}-4=0\)
\(\Leftrightarrow1+tan^2x-tanx\left(1+tan^2x\right)-4=0\)
\(\Leftrightarrow-tan^3x+tan^2x-tanx-3=0\)
\(\Leftrightarrow\left(tanx+1\right)\left(tan^2x-2tanx+3\right)=0\)
\(\Leftrightarrow tanx=-1\Rightarrow x=-\frac{\pi}{4}+k\pi\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
a) 1-cot^4xfrac{2}{sin^2x}-frac{1}{sin^4x}b)frac{1-2sinx.cosx}{cos^2-sin^2}frac{1-tanx}{1+tanx}c)frac{sin^2x}{sinx-cosx}+frac{sinx+cosx}{1-tanx}sinx+cosxd)sqrt{frac{1+cosx}{1-cosx}}-sqrt{frac{1-cosx}{1+cosx}}frac{2.cosx}{|sin|}e)tan^3x+tan^2x+tanx+1frac{sinx+cosx}{cos^3x}
Đọc tiếp
a) \(1-cot^4x=\frac{2}{sin^2x}-\frac{1}{sin^4x}\)
b)\(\frac{1-2sinx.cosx}{cos^2-sin^2}\)\(=\frac{1-tanx}{1+tanx}\)\(\)
c)\(\frac{sin^2x}{sinx-cosx}+\frac{sinx+cosx}{1-tanx}=sinx+cosx\)
d)\(\sqrt{\frac{1+cosx}{1-cosx}}-\sqrt{\frac{1-cosx}{1+cosx}}=\frac{2.cosx}{|sin|}\)
e)\(tan^3x+tan^2x+tanx+1=\frac{sinx+cosx}{cos^3x}\)
Bài 1 : Chứng minh rằng
a) frac{1-sinx}{cosx}frac{cosx}{1+sinx}
b) frac{tanx}{sinx}-frac{sinx}{cotx}cosx
Bài 2 : Chứng minh các biểu thức sau độc lập với biến x
A frac{cot^2x-cos^2x}{cot^2x}+frac{sinxcosx}{cotx}
B cos^4x+sin^2xcos^2x+sin^{2^{ }}x
Bài 3 : Tính giá trị các biểu thức lượng giác
Afrac{5cosx+6tanx}{5cosx-6tanx} biết tanx2
B frac{4sinxcosx-3cos^2x}{^{ }1+3sin^2x} biết cotx -6
Bài 4 : Tính giá trị các biểu thức lượng giác
A frac{cotx}{cotx-tanx} biết sinxfrac{3}{5} với 0...
Đọc tiếp
Bài 1 : Chứng minh rằng
a) \(\frac{1-sinx}{cosx}=\frac{cosx}{1+sinx}\)
b) \(\frac{tanx}{sinx}-\frac{sinx}{cotx}=cosx\)
Bài 2 : Chứng minh các biểu thức sau độc lập với biến x
A= \(\frac{cot^2x-cos^2x}{cot^2x}+\frac{sinxcosx}{cotx}\)
B= \(cos^4x+sin^2xcos^2x+sin^{2^{ }}x\)
Bài 3 : Tính giá trị các biểu thức lượng giác
A=\(\frac{5cosx+6tanx}{5cosx-6tanx}\) biết tanx=2
B= \(\frac{4sinxcosx-3cos^2x}{^{ }1+3sin^2x}\) biết cotx = -6
Bài 4 : Tính giá trị các biểu thức lượng giác
A= \(\frac{cotx}{cotx-tanx}\) biết sinx=\(\frac{3}{5}\) với \(0^o< x\le90^o\)
B= sina+cosa tana biết cosa=\(\frac{1}{2}\) với \(\frac{3\pi}{2}< a< 2\pi\)
Bài 5 : Tính giá trị lượng giác còn lại của góc 2a nếu :
a) cos2\(\alpha\) = \(\frac{2}{5}\) biết \(0< \alpha< \frac{\pi}{4}\)
b) sin2\(\alpha\) = \(\frac{24}{25}\) biết \(\frac{-3\pi}{4}\le\alpha\le-\frac{\pi}{2}\)
Bài 1:
\(\frac{1-sinx}{cosx}=\frac{cosx\left(1-sinx\right)}{cos^2x}=\frac{cosx\left(1-sinx\right)}{1-sin^2x}=\frac{cosx\left(1-sinx\right)}{\left(1-sinx\right)\left(1+sinx\right)}=\frac{cosx}{1+sinx}\)
\(\frac{tanx}{sinx}-\frac{sinx}{cotx}=\frac{tanx.cotx-sin^2x}{sinx.cotx}=\frac{1-sin^2x}{cosx}=\frac{cos^2x}{cosx}=cosx\)
Bài 2:
\(A=\frac{cot^2x-cos^2x}{cot^2x}+\frac{sinx.cosx}{cotx}=\frac{sin^2x\left(cot^2x-cos^2x\right)}{cos^2x}+\frac{sinx.sinx.cosx}{cosx}\)
\(=\frac{cos^2x-cos^2x.sin^2x}{cos^2x}+sin^2x=1-sin^2x+sin^2x=1\)
\(B=cos^2x\left(cos^2x+sin^2x\right)+sin^2x=cos^2x+sin^2x=1\)
Bài 3:
A đề đúng chứ bạn? Là cos hay cot?
\(B=\frac{\frac{4sinx.cosx}{sin^2x}-\frac{3cos^2x}{sin^2x}}{\frac{1}{sin^2x}+3}=\frac{4cotx-3cot^2x}{1+cot^2x+3}=\frac{4.\left(-6\right)-3.\left(-6\right)^2}{1+\left(-6\right)^2+3}=...\)
Đúng 0
Bình luận (0)
Bài 4:
\(0< x< 90^0\Rightarrow cosx>0\)
\(\Rightarrow cosx=\sqrt{1-sin^2x}=\frac{4}{5}\)
\(tanx=\frac{sinx}{cosx}=\frac{3}{4}\) ; \(cotx=\frac{1}{tanx}=\frac{4}{3}\)
\(\Rightarrow A=\frac{\frac{4}{3}}{\frac{4}{3}-\frac{3}{4}}=\frac{16}{7}\)
\(\frac{3\pi}{2}< a< 2\pi\Rightarrow sina< 0\)
\(\Rightarrow sina=-\sqrt{1-cos^2a}=-\frac{\sqrt{3}}{2}\)
\(B=sina+cosa=\frac{1-\sqrt{3}}{2}\)
Bài 5:
\(0< a< \frac{\pi}{4}\Rightarrow0< 2a< \frac{\pi}{2}\Rightarrow sin2a>0\)
\(\Rightarrow sin2a=\sqrt{1-cos^2a}=\frac{\sqrt{21}}{5}\)
\(tan2a=\frac{sin2a}{cos2a}=\frac{\sqrt{21}}{2}\)
\(cot2a=\frac{1}{tan2a}=\frac{2\sqrt{21}}{21}\)
b/ \(-\frac{3\pi}{4}\le a\le-\frac{\pi}{2}\Rightarrow-\frac{3\pi}{2}\le2a\le-\pi\Rightarrow cos2a< 0\)
\(\Rightarrow cos2a=-\sqrt{1-sin^2a}=-\frac{7}{25}\)
\(tan2a=\frac{sin2a}{cos2a}=-\frac{24}{7}\)
\(cot2a=\frac{1}{tan2a}=-\frac{7}{24}\)
Đúng 0
Bình luận (0)
Bài 1:
a)
ĐK: $\cos x\neq 0$ $\Rightarrow \sin x\neq -1$. Ta có:
\(\frac{1-\sin x}{\cos x}=\frac{(1-\sin x)(1+\sin x)}{\cos x(1+\sin x)}=\frac{1-\sin ^2x}{\cos x(1+\sin x)}=\frac{\cos ^2x}{\cos x(1+\sin x)}=\frac{\cos x}{1+\sin x}\)
(đpcm)
b) ĐK: $\sin x; \cos x\neq 0$
\(\frac{\tan x}{\sin x}-\frac{\sin x}{\cot x}=\frac{\tan x\cot x-\sin ^2x}{\sin x\cot x}=\frac{1-\sin ^2x}{\sin x.\cot x}=\frac{\cos ^2x}{\sin x.\frac{\cos x}{\sin x}}=\frac{\cos ^2x}{\cos x}=\cos x\) (đpcm)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời