Bài 4: Trong mặt phẳng Oxy, viết phương trình đường thẳng AB trong các trường hợp:
a) A(-1; 1) và B(2; 4)
b) A(0; -1) và B(1; 0
Bài tập 6. Trong mặt phẳng Oxy, cho hai đường thẳng Delta_{1} / 2 * x - y - 2 = 0 , Delta_{2} / x - y + 3 = 0 và hai điểm A(-1;3) , B(0;2) . a. Viết phương trình đường thẳng qua AB. b. Viết phương trình đường thẳng trung trực của đoạn thẳng AB . c. Viết phương trình đường thẳng qua 4 và song song với Delta_{1} . d. Viết phương trình đường thẳng qua 4 và vuông góc với Delta_{1} e. Viết phương trình đường thẳng qua B và có hệ số góc k = - 3 . f. Tính côsin góc giữa hai đường thẳng Delta_{1}, Delta_{2} g. Tính d(A, Delta_{2}) . h. Viết phương trình đường thẳng qua 4 và tạo với Delta_{1} một góc c biết cos varphi = 1/(sqrt(5)) i. Tìm tọa độ hình chiếu vuông góc của 4 trên Delta_{2} j. Tìm tọa độ điểm B^ prime d hat oi xứng với B qua Delta_{2}
Câu 3: Trong mặt phẳng Oxy, cho hai điểm A(1;-2), B(3;1). Viết phương trình tham số của đường thẳng d đi qua hai điểm A và B.
Câu 4: Cho hai điểm A(4; -3), B(2;1). Viết phương trình đường tròn (C) nhận AB làm đường kính
Câu 4:
Tọa độtâm I là;
x=(4+2)/2=3 và y=(-3+1)/2=-1
I(3;-1); A(4;-3)
IA=căn (4-3)^2+(-3+1)^2=căn 5
=>(C): (x-3)^2+(y+1)^2=5
Câu 3:
vecto AB=(2;3)
PTTS là:
x=1+2t và y=-2+3t
Bài 5. Trong mặt phẳng Oxy, cho điểm A(2;-1) và đường thẳng d : 3x-4y+5=0
a) Viết phương trình đường thẳng đi qua A và vuông góc với d
b) Viết phương trình đường thẳng đi qua A và song song với d.
c) Viết phương trình đường thẳng song song với d và cách A một khoảng bằng 3
Gọi đường thẳng đi qua A là d'.
a) Ta có: \(d'\perp d.\)
\(\Rightarrow\) VTPT của d là VTCP của d'.
Mà VTPT của d là: \(\overrightarrow{n_d}=\left(3;-4\right).\)
\(\Rightarrow\overrightarrow{u_{d'}}=\left(3;-4\right).\Rightarrow\overrightarrow{n_{d'}}=\left(4;3\right).\)
\(\Rightarrow\) Phương trình đường thẳng d' là:
\(4\left(x-2\right)+3\left(y+1\right)=0.\\ \Leftrightarrow4x+3y-5=0.\)
b) Ta có: \(d'//d.\)
\(\Rightarrow\) VTPT của d là VTPT của d'.
Mà VTPT của d là: \(\overrightarrow{n_d}=\left(3;-4\right).\)
\(\Rightarrow\) \(\overrightarrow{n_{d'}}=\left(3;-4\right).\)
\(\Rightarrow\) Phương trình đường thẳng d' là:
\(3\left(x-2\right)-4\left(y+1\right)=0.\\ \Leftrightarrow3x-4y-10=0.\)
Trong mặt phẳng tọa độ Oxy cho A (4;5), B(1;-1), C(4;-4), D(7;-1) (vẽ hình nhé)
a) Viết phương trình đường thẳng AB, CD, DA
b) Tính chu vi tứ giác ABCD
Để viết phương trình đường thẳng AB, ta cần tìm được độ dốc và điểm qua của đường thẳng. Để tính chu vi tứ giác ABCD, ta cần tính độ dài các cạnh và tổng các cạnh.
a) Để viết phương trình đường thẳng AB, ta cần tính độ dốc và điểm qua của đường thẳng. Để tính độ dốc, ta sử dụng công thức: m = (y2 - y1) / (x2 - x1), với (x1, y1) và (x2, y2) là hai điểm trên đường thẳng. Ta có A(4, 5) và B(1, -1), áp dụng công thức, ta tính được độ dốc của đường thẳng AB là m = (5 - (-1)) / (4 - 1) = 2.
Để tìm điểm qua của đường thẳng AB, ta có thể sử dụng một trong hai điểm đã cho. Ví dụ, ta sử dụng điểm A(4, 5). Áp dụng công thức: y - y1 = m(x - x1), ta có phương trình đường thẳng AB là y - 5 = 2(x - 4).
Tương tự, để viết phương trình đường thẳng CD, ta tính độ dốc và điểm qua của đường thẳng. Ta có C(4, -4) và D(7, -1), áp dụng công thức, ta tính được độ dốc của đường thẳng CD là m = (-1 - (-4)) / (7 - 4) = 1.
Để tìm điểm qua của đường thẳng CD, ta có thể sử dụng một trong hai điểm đã cho. Ví dụ, ta sử dụng điểm C(4, -4). Áp dụng công thức: y - y1 = m(x - x1), ta có phương trình đường thẳng CD là y - (-4) = 1(x - 4).
b) Để tính chu vi tứ giác ABCD, ta cần tính độ dài các cạnh và tổng các cạnh. Ta có A(4, 5), B(1, -1), C(4, -4), D(7, -1). Để tính độ dài cạnh AB, ta sử dụng công thức khoảng cách giữa hai điểm: AB = √((x2 - x1)^2 + (y2 - y1)^2). Áp dụng công thức, ta tính được AB = √((1 - 4)^2 + (-1 - 5)^2) = √((-3)^2 + (-6)^2) = √(9 + 36) = √45.
Tương tự, ta tính được CD = √((7 - 4)^2 + (-1 - (-4))^2) = √(3^2 + 3^2) = √(9 + 9) = √18.
Để tính chu vi tứ giác ABCD, ta cộng tổng độ dài các cạnh: chu vi = AB + BC + CD + DA = √45 + BC + √18 + DA.
Tuy nhiên, để tính độ dài cạnh BC và DA, cần có thêm thông tin về các điểm trên đường thẳng BC và DA. Vì vậy, để tính chu vi tứ giác ABCD, cần có thêm thông tin.
Trong mặt phẳng tọa độ Oxy cho A (4;5), B(1;-1), C(4;-4), D(7;-1) (vẽ hình nhé)
a) Viết phương trình đường thẳng AB, CD, DA
b) Tính chu vi tứ giác ABCD
a) Để viết phương trình đường thẳng AB, CD, DA, ta có thể sử dụng công thức phương trình đường thẳng đi qua hai điểm.
Phương trình đường thẳng AB: Điểm A(4,5) và B(1,-1) Ta có: Độ dốc của đường thẳng AB: m = (y2 - y1) / (x2 - x1) = (-1 - 5) / (1 - 4) = -2 Phương trình đường thẳng AB: y - y1 = m(x - x1) => y - 5 = -2(x - 4) => y - 5 = -2x + 8 => 2x + y = 13
Phương trình đường thẳng CD: Điểm C(4,-4) và D(7,-1) Ta có: Độ dốc của đường thẳng CD: m = (y2 - y1) / (x2 - x1) = (-1 - (-4)) / (7 - 4) = 1 Phương trình đường thẳng CD: y - y1 = m(x - x1) => y - (-1) = 1(x - 7) => y + 1 = x - 7 => x - y = 8
Phương trình đường thẳng DA: Điểm D(7,-1) và A(4,5) Ta có: Độ dốc của đường thẳng DA: m = (y2 - y1) / (x2 - x1) = (5 - (-1)) / (4 - 7) = -2 Phương trình đường thẳng DA: y - y1 = m(x - x1) => y - (-1) = -2(x - 7) => y + 1 = -2x + 14 => 2x + y = 13
b) Để tính chu vi tứ giác ABCD, ta cần tính độ dài các cạnh của tứ giác.
Độ dài cạnh AB: AB = √[(x2 - x1)^2 + (y2 - y1)^2] = √[(1 - 4)^2 + (-1 - 5)^2] = √[9 + 36] = √45
Độ dài cạnh BC: BC = √[(x2 - x1)^2 + (y2 - y1)^2] = √[(4 - 1)^2 + (-4 - (-1))^2] = √[9 + 9] = √18
Độ dài cạnh CD: CD = √[(x2 - x1)^2 + (y2 - y1)^2] = √[(7 - 4)^2 + (-1 - (-4))^2] = √[9 + 9] = √18
Độ dài cạnh DA: DA = √[(x2 - x1)^2 + (y2 - y1)^2] = √[(7 - 4)^2 + (-1 - 5)^2] = √[9 + 36] = √45
Từ đó, chu vi tứ giác ABCD là: AB + BC + CD + DA = √45 + √18 + √18 + √45.
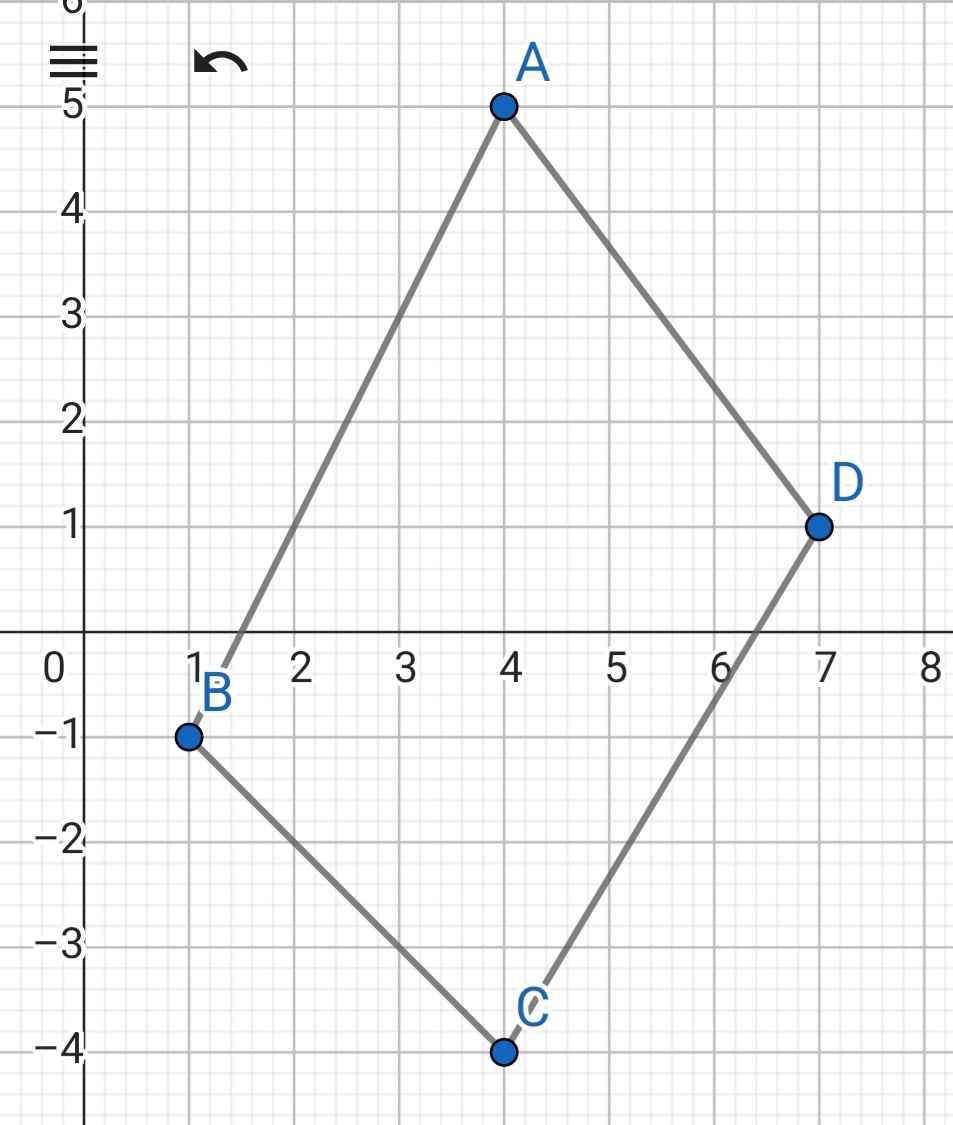 a) * Gọi (d): y = ax + b là phương trình đường thẳng AB
a) * Gọi (d): y = ax + b là phương trình đường thẳng AB
Do (d) đi qua A nên:
4a + b = 5
⇔ b = 5 - 4a (1)
Do (d) đi qua B nên:
a + b = -1 (2)
Thay (1) vào (2) ta được:
a + 5 - 4a = -1
⇔ -3a = -6
⇔ a = 2
Thay a = 2 vào (1) ta được:
b = 5 - 4.2 = -3
Vậy (d): y = 2x - 3
* Gọi (d'): y = ax + b là phương trình đường thẳng CD
Do (d') đi qua C nên:
4a + b = -4
⇔ b = -4 - 4a (3)
Do (d') đi qua D nên:
7a + b = -1 (4)
Thay (3) vào (4) ta được:
7a - 4 - 4a = -1
⇔ 3a = 3
⇔ a = 1
Thay a = 1 vào (3) ta được:
b = -4 - 4.1 = -8
Vậy (d'): y = x - 8
* Gọi (d''): y = ax + b là phương trình đường thẳng DA
Do (d'') di qua D nên:
7a + b = -1
⇔ b = -1 - 7a (5)
Do (d'') đi qua A nên:
4a + b = 5 (6)
Thay (5) vào (6) ta được:
4a - 1 - 7a = 5
⇔ -3a = 6
⇔ a = -2
Thay a = -2 vào (5) ta được:
b = -1 - 7.(-2) = 13
Vậy (d''): y = -2x + 13
b) Ta có:
AB² = 3² + 6² = 45
⇒ AB = 3√5
BC² = 3² + 3² = 18
⇒ BC = 3√2
CD² = 3² + 5² = 34
⇒ CD = √34
AD² = 3² + 4² = 25
⇒ AD = 5
Chu vi tứ giác ABCD:
3√5 + 3√2 + √34 + 5
Trong mặt phẳng Oxy, cho tam giác ABC với A(3;1), B(0;5), C(6;1).
a) Viết phương trình tổng quát của đường thẳng AB.
b) Viết phương trình đường tròn (C) tâm C tiếp xúc với đường thẳng AB
\(\overrightarrow{AB}=\left(-3;4\right)\Rightarrow\) đường thẳng AB nhận \(\left(4;3\right)\) là 1 vtpt
Phương trình AB:
\(4\left(x-3\right)+3\left(y-1\right)=0\Leftrightarrow4x+3y-15=0\)
b.
\(R=d\left(C;AB\right)=\dfrac{\left|4.6+1.3-15\right|}{\sqrt{4^3+3^2}}=\dfrac{12}{5}\)
Phương trình (C):
\(\left(x-6\right)^2+\left(y-1\right)^2=\dfrac{144}{25}\)
Trong mặt phẳng với hệ tọa độ Oxy Cho điểm A(1;-2) và B(3;4)
Viết phương trình tham số của đường thẳng AB
Trong mặt phẳng Oxy cho ba điểm A(-6;3), B(0;-1), C(3;2) a) Viết phương trình tham số với đường thẳng AB b) Viết phương trình đường thẳng d đi qua C và vuông góc với đường thẳng AB c) Tìm tọa độ điểm m trên đường thẳng d 2x- y + 3 = 0 sao cho | vectơ MA + vectơ MB + MC| nhỏ nhất
Trong mặt phẳng Oxy cho ba điểm A(-6;3), B(0;-1), C(3;2) a) Viết phương trình tham số với đường thẳng AB b) Viết phương trình đường thẳng d đi qua C và vuông góc với đường thẳng AB c) Tìm tọa độ điểm m trên đường thẳng d 2x- y + 3 = 0 sao cho | vectơ MA + vectơ MB + MC| nhỏ nhất
a: vecto AB=(6;-4)
PTTS là:
x=-6+6t và y=3-4t
b: Vì (d) vuông góc AB nên (d) có VTPT là (3;-2)
Phương trình(d) là:
3(x-3)+(-2)(y-2)=0
=>3x-9-2y+4=0
=>3x-2y-5=0