a) Để viết phương trình đường thẳng AB, CD, DA, ta có thể sử dụng công thức phương trình đường thẳng đi qua hai điểm.
Phương trình đường thẳng AB: Điểm A(4,5) và B(1,-1) Ta có: Độ dốc của đường thẳng AB: m = (y2 - y1) / (x2 - x1) = (-1 - 5) / (1 - 4) = -2 Phương trình đường thẳng AB: y - y1 = m(x - x1) => y - 5 = -2(x - 4) => y - 5 = -2x + 8 => 2x + y = 13
Phương trình đường thẳng CD: Điểm C(4,-4) và D(7,-1) Ta có: Độ dốc của đường thẳng CD: m = (y2 - y1) / (x2 - x1) = (-1 - (-4)) / (7 - 4) = 1 Phương trình đường thẳng CD: y - y1 = m(x - x1) => y - (-1) = 1(x - 7) => y + 1 = x - 7 => x - y = 8
Phương trình đường thẳng DA: Điểm D(7,-1) và A(4,5) Ta có: Độ dốc của đường thẳng DA: m = (y2 - y1) / (x2 - x1) = (5 - (-1)) / (4 - 7) = -2 Phương trình đường thẳng DA: y - y1 = m(x - x1) => y - (-1) = -2(x - 7) => y + 1 = -2x + 14 => 2x + y = 13
b) Để tính chu vi tứ giác ABCD, ta cần tính độ dài các cạnh của tứ giác.
Độ dài cạnh AB: AB = √[(x2 - x1)^2 + (y2 - y1)^2] = √[(1 - 4)^2 + (-1 - 5)^2] = √[9 + 36] = √45
Độ dài cạnh BC: BC = √[(x2 - x1)^2 + (y2 - y1)^2] = √[(4 - 1)^2 + (-4 - (-1))^2] = √[9 + 9] = √18
Độ dài cạnh CD: CD = √[(x2 - x1)^2 + (y2 - y1)^2] = √[(7 - 4)^2 + (-1 - (-4))^2] = √[9 + 9] = √18
Độ dài cạnh DA: DA = √[(x2 - x1)^2 + (y2 - y1)^2] = √[(7 - 4)^2 + (-1 - 5)^2] = √[9 + 36] = √45
Từ đó, chu vi tứ giác ABCD là: AB + BC + CD + DA = √45 + √18 + √18 + √45.
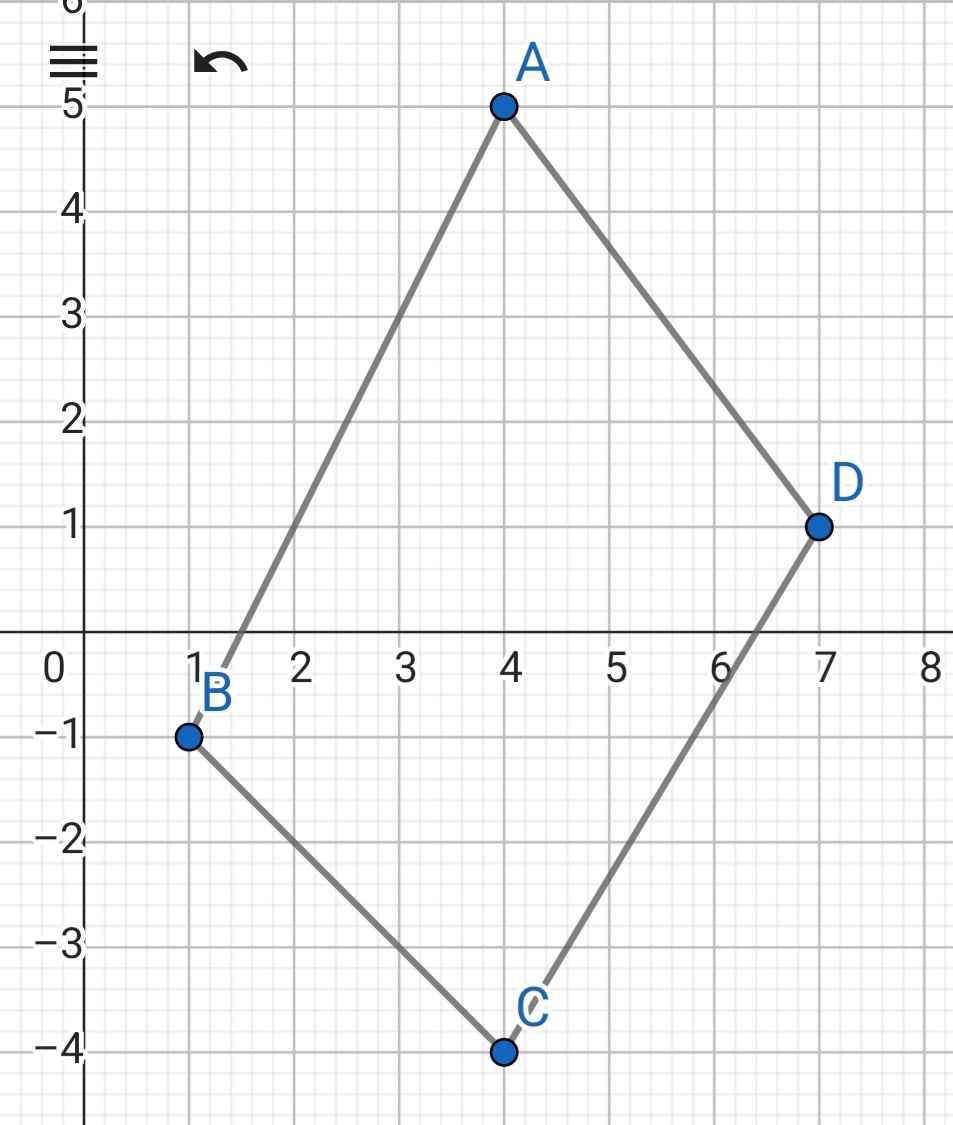a) * Gọi (d): y = ax + b là phương trình đường thẳng AB
Do (d) đi qua A nên:
4a + b = 5
⇔ b = 5 - 4a (1)
Do (d) đi qua B nên:
a + b = -1 (2)
Thay (1) vào (2) ta được:
a + 5 - 4a = -1
⇔ -3a = -6
⇔ a = 2
Thay a = 2 vào (1) ta được:
b = 5 - 4.2 = -3
Vậy (d): y = 2x - 3
* Gọi (d'): y = ax + b là phương trình đường thẳng CD
Do (d') đi qua C nên:
4a + b = -4
⇔ b = -4 - 4a (3)
Do (d') đi qua D nên:
7a + b = -1 (4)
Thay (3) vào (4) ta được:
7a - 4 - 4a = -1
⇔ 3a = 3
⇔ a = 1
Thay a = 1 vào (3) ta được:
b = -4 - 4.1 = -8
Vậy (d'): y = x - 8
* Gọi (d''): y = ax + b là phương trình đường thẳng DA
Do (d'') di qua D nên:
7a + b = -1
⇔ b = -1 - 7a (5)
Do (d'') đi qua A nên:
4a + b = 5 (6)
Thay (5) vào (6) ta được:
4a - 1 - 7a = 5
⇔ -3a = 6
⇔ a = -2
Thay a = -2 vào (5) ta được:
b = -1 - 7.(-2) = 13
Vậy (d''): y = -2x + 13
b) Ta có:
AB² = 3² + 6² = 45
⇒ AB = 3√5
BC² = 3² + 3² = 18
⇒ BC = 3√2
CD² = 3² + 5² = 34
⇒ CD = √34
AD² = 3² + 4² = 25
⇒ AD = 5
Chu vi tứ giác ABCD:
3√5 + 3√2 + √34 + 5