số x dương mà x/3 = 3/4x
AN
Những câu hỏi liên quan
Cho hàm số
f
(
x
)
x
2
-
4
x
-
2
2
x
+
3
. Tìm khoảng...
Đọc tiếp
Cho hàm số f ( x ) = x 2 - 4 x - 2 2 x + 3 . Tìm khoảng mà trong đó f(x) nhận giá trị dương
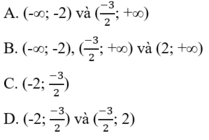
Cách 1. Lập bảng xét dấu.
Cách 2. f(x) không xác định khi x = 2 và 2 ∈ ((-3)/2; +∞) nên A sai. Dễ thấy x = (-7)/4 thì x 2 – 4 < 0; x – 2 < 0; 2x + 3 < 0 ⇒ f(x) < 0, vì vậy C và D sai.
Đáp án: B
Đúng 0
Bình luận (0)
Tính GTNN của P= \(4x-\frac{4\sqrt{x}+3}{x+1}+\frac{1}{4x}+2017\)
với x là một số thực dương
tìm x là nghiệm nguyên dương của phương trình \(\frac{x^2\left(4x^6-2x^3+1\right)}{12^{x^2-4x+3}}=\frac{8x^9+1}{6^{x^2-4x+3}+8^{x^2-4x+3}+9^{x^2+4x+3}}\)
x=+-10;x=1+431/1000;x=-1893/2500;x=-7543/10000;x=1
Đúng 0
Bình luận (0)
x=0,+-10 ms biết như thế ko biết đúng ko
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
tìm x,a,b là số nguyên dương biết 4x+19=3^a và 2x+5=3^b
cho 2 số dương x;y thỏa mãn điều kiện: \(x+y\le1\)
chứng minh: \(x^2-\dfrac{3}{4x}-\dfrac{x}{y}\le\dfrac{-9}{4}\)
Ta có \(x+y\le1\Leftrightarrow1-x\ge y>0\Leftrightarrow0< x< 1\)
Giả sử \(x^2-\dfrac{3}{4x}-\dfrac{x}{y}\le-\dfrac{9}{4}\)
\(\Leftrightarrow4x^2+9\le\dfrac{3}{x}+\dfrac{4x}{y}\\ \Leftrightarrow\dfrac{4x}{1-x}+\dfrac{3}{x}\ge4x^2+9\\ \Leftrightarrow\dfrac{4x^2+3\left(1-x\right)-x\left(4x^2+9\right)\left(1-x\right)}{x\left(1-x\right)}\ge0\\ \Leftrightarrow\dfrac{4x^4-4x^3+13x^2-12x+3}{x\left(1-x\right)}\ge0\\ \Leftrightarrow\dfrac{\left(x^2+3\right)\left(2x-1\right)^2}{x\left(1-x\right)}\ge0\)
Vì \(x>0;1-x>0\) nên BĐT trên luôn đúng
Vậy ta được đpcm
Dấu \("="\Leftrightarrow x=y=\dfrac{1}{2}\)
Đúng 0
Bình luận (0)
Cho 2 số thực dương x,y thỏa mãn
\(x^3+y^3-3xy\left(x^2+y^2\right)+4x^2y^2\left(x+y\right)-4x^3y^3=0\)
Tìm giá trị nhỏ nhất của biểu thức M=x+y
Cho các số dương x,y thỏa 4x+5y=7 . Tìm GTNN của biểu thức \(B=5\left|x\right|-3\left|y\right|\)
Tìm các số nguyên dương x, a, b biết: 4x+19=3a, 2x+5=3b
y=2x+5
y=3^a-9
y=3^b
3^a-3^2=3^b
\(3^2.\left(3^{a-2}-1\right)=3^b\Rightarrow3^{a-2}-1=1\left(duynhat\right)\)
a=2=> b=2
=> y=9=> x=2
Đúng 0
Bình luận (0)
Cho các hàm số sau: \(y=\dfrac{1}{3}x^3-x^2+3x+4\); \(y=\sqrt{x^2+4}\);\(y=x^3+4x-sinx\);\(y=x^4+x^2+2\). Có bao nhiêu hàm số đồng biến trên những khoảng mà nó xác định
y'=1/3*3x^2-2x+3=x^2-2x+3=(x-1)^2+2>0
=>y=1/3x^3-x^2+3x+4 luôn đồng biến trên từng khoảng xác định
\(y=\sqrt{x^2+4}\)
=>\(y'=\dfrac{-\left(x^2+4\right)'}{\left(x^2+4\right)^2}=\dfrac{-\left(2x\right)}{\left(x^2+4\right)^2}\)
=>Hàm số này không đồng biến trên từng khoảng xác định
\(y=x^3+4x-sinx\)
=>y'=3x^2+4-cosx
-1<=-cosx<=1
=>3<=-cosx+4<=5
=>y'>0
=>Hàm số luôn đồng biến trên từng khoảng xác định
y=x^4+x^2+2
=>y'=4x^3+2x=2x(2x^2+1)
=>Hàm số ko đồng biến trên từng khoảng xác định
Đúng 1
Bình luận (0)



