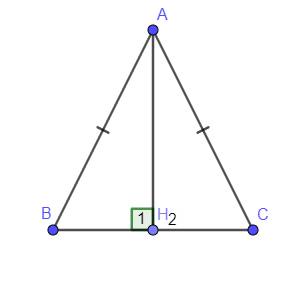
Cho tam giác ABC cân tại A. Vẽ AH ⊥ BC
a) Chứng minh: AHB = AHC; b)Vẽ HM ⊥ AB, HN ⊥ AC. Chứng minh AMN cân
c) Chứng minh MN // BC; d)Chứng minh AH2 + BM2 = AN2 +BH2
Giúp mình câu d thôi nhé cảm ơn nhiều