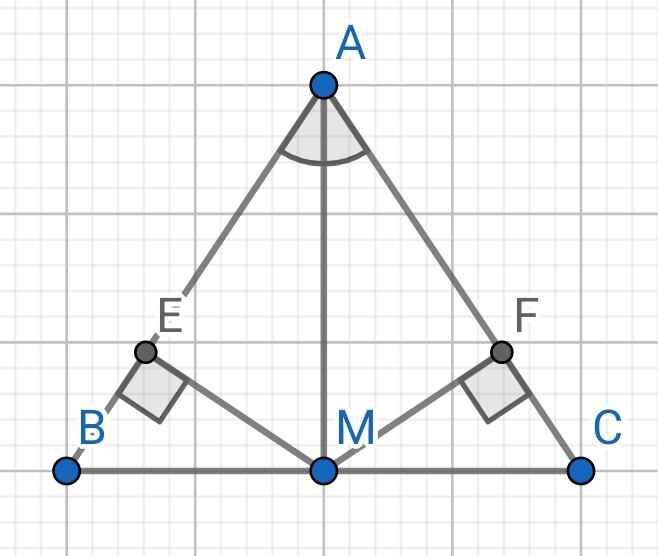
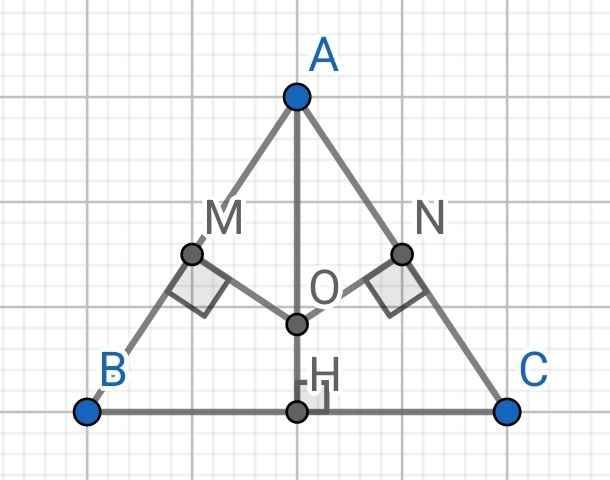
Cho tam giác ABC có AB=AC, AM là phân giác của góc BAC ( M thuộc BC ):
a, Chứng minh tam giác ABM= tam giác ACM
b, Chứng minh M là trung điểm của BC và AM vuông góc BC
c, Kẻ ME vuông góc AB ( E thuộc AB ) và MF vuông góc AC ( F thuộc AC ). Chứng minh ME=MF
a) Do AM là tia phân giác của ∠BAC (gt)
⇒ ∠BAM = ∠CAM
Xét ∆ABM và ∆ACM có:
AB = AC (gt)
∠BAM = ∠CAM (cmt)
AM là cạnh chung
⇒ ∆ABM = ∆ACM (c-g-c)
b) Do ∆ABM = ∆ACM (cmt)
⇒ BM = CM (hai cạnh tương ứng)
⇒ M là trung điểm của BC
Do ∆ABM = ∆ACM (cmt)
⇒ ∠AMB = ∠AMC (hai góc tương ứng)
Mà ∠AMB + ∠AMC = 180⁰ (kề bù)
⇒ ∠AMB = ∠AMC = 180⁰ : 2 = 90⁰
⇒ AM ⊥ BC
c) Do ∠BAM = ∠CAM (cmt)
⇒ ∠EAM = ∠FAM
Xét hai tam giác vuông: ∆AME và ∆AMF có:
AM là cạnh chung
∠EAM = ∠FAM (cmt)
⇒ ∆AME = ∆AMF (cạnh huyền góc nhọn)
⇒ ME = MF (hai cạnh tương ứng)
a,
Xét tam giác ABC có:
+ AB = AC (giả thuyết)
+ Góc CAM = MAB (AM là phân giác góc BAC)
+ AM chung
⇒ 2 tam giác bằng nhau (cgc) (đpcm)
b,
Ta có:
+ Tam giác AMC = Tam giác ABM (theo câu a)
⇒ CM = MB (2 cạnh tương ứng) (1)
⇒ M là trung điểm BC (đpcm)
+ Mà AM là tia phân giác góc CAB (2)
+ Góc AMC = Góc AMB (3)
Từ (1), (2), (3).
⇒ AM ⊥ BC (t/c) (đpcm)
c,
Ta có:
Tam giác ACM = Tam giác ABM (theo câu A)
⇒ Góc ACM = Góc ABM (2 góc tương ứng)
Ta có:
+ ME ⊥ AB (giả thuyết)
⇒ Tam giác MEB vuông tại E
+ MF ⊥ AC (giả thuyết)
⇒ Tam giác CFM vuông tại F
Xét tam giác CFM vuông tại F và tam giác MEB vuông tại E có:
+ Góc ACM bằng góc ABM (chứng minh trên)
+ MC = MB (theo câu b)
⇒ Hai tam giác CFM = MEB (cạnh huyền góc nhọn)
⇒ ME = MF (hai cạnh tương ứng) (đpcm)
Cho tam giac ABC,có AC>AB,trên hai cạnh AB và AC theo thứ tự lấy D và E sao cho BD=CE. c/m DC>DE
Cho tam giác ABC cân tại A.Trên cạnh AB,AC lần lượt lấy các điểm K,H sao cho AK=AH . Gọi O là giao điểm của BH và CK . Chứng minh tam giác OBC cân
có vẽ hình nhé
Vì \(\Delta\)ABC cân tại A \(\rightarrow AB=AC;\widehat{ABC}=\widehat{ACB}\)
Xét \(\Delta AHB\) và \(\Delta AKC\) có:
\(\widehat{A}\) chung
AH=AK (gt)
AB=AC
\(\rightarrow\Delta AHB=\Delta AKC\left(cgc\right)\)
\(\rightarrow\widehat{ABH}=\widehat{ACK}\) (2 góc tương ứng)
Ta có: \(\widehat{ABC}=\widehat{OBC}+\widehat{ABH}\); \(\widehat{ACB}=\widehat{OCB}+\widehat{ACK}\)
\(\widehat{ABC}+\widehat{ACB}\rightarrow\widehat{OBC}+\widehat{ABH}=\widehat{OCB}+\widehat{ACK}\)
mà \(\widehat{ABH}=\widehat{ACK}\)
\(\rightarrow\widehat{OBC}=\widehat{OCB}\)
\(\Rightarrow\Delta OBC\) cân tại O (đpcm)
cho tam giác abc cân tại a tia pg góc b cắt mạnh ac tại dtia pg góc c cắt mạnh ab tại e . cm ade cân
CHO ΔABC CÓ AB= AC VÀ AB≥ BC GỌI M LÀ TRUNG ĐIỂM CỦA CẠNH BC A/ CHỨNG MINH Δ ABM = Δ ACM VÀ AM VUÔNG BC B/ TRÊN CẠNH AB LẤY ĐIỂM D TRÊN CẠNH AC LẤY ĐIỂM E SAO CHO AD = AE CHỨNG MINH Δ MDE CÂN
cho Δ ABC cân tại A lấy điểm D thuộc cạnh AC điểm E thuộc cạnh AB sao cho AD = AE A/ SO sánh ABD = ACE B/ Gọi I là giao điểm của BD và CE Tam giác IBC là tam giác gì vì sao ? C/ chứng minh ED//BC
kẻ bd vuông ac . ce vuong ab d thuộc ac , e thuộc ab chứng minh be= cd
Đề không đầy đủ. Bạn xem lại nhé.
cho tam giác ABC cân tại A .Tính góc B
Đề chưa đủ dữ kiện đâu em
Cho tam giác ABC cân tại A. Gọi M, N là trung điểm các cạnh AB, AC. Các đường thẳng vuông góc với AB, AC tại M; N cắt nhau tại điểm O, AO cắt BC tại H. Chứng minh HB=HC và AH vuông góc với BC
Do OM ⊥ AB (gt)
⇒ OM là đường cao của ∆ABC
Do ON ⊥ AC (gt)
⇒ ON là đường cao của ∆ABC
⇒ O là giao điểm của hai đường cao của ∆ABC
⇒ AO là đường cao thứ ba
⇒ AH ⊥ BC
Xét hai tam giác vuông: ∆ABH và ∆ACH có:
AH là cạnh chung
AB = AC (do ∆ABC cân tại A)
⇒ ∆ABH = ∆ACH (cạnh huyền - cạnh góc vuông)
⇒ HB = HC (hai cạnh tương ứng)
a: Xét ΔBAD vuông tại A và ΔBHD vuông tại H có
BD chung
\(\widehat{ABD}=\widehat{HBD}\)
Do đó: ΔBAD=ΔBHD
=>BA=BH
b: Ta có: ΔBAD=ΔBHD
=>DA=DH
Ta có: DA=DH
DH<DC(ΔDHC vuông tại H)
Do đó: DA<DC
c: Xét ΔBHI vuông tại H và ΔBAC vuông tại A có
BH=BA
\(\widehat{HBI}\) chung
Do đó: ΔBHI=ΔBAC
=>BI=BC
=>ΔBIC cân tại B
d: Ta có: ΔBHI=ΔBAC
=>HI=AC
Ta có: AD+DC=AC
HD+DI=HI
mà AC=HI và AD=HD
nên DC=DI
=>D nằm trên đường trung trực của CI(1)
ta có: BI=BC
=>B nằm trên đường trung trực của CI(2)
ta có: MI=MC
=>M nằm trên đường trung trực của CI(3)
từ (1),(2),(3) suy ra B,M,D thẳng hàng
