Cho ba điểm A( 2 ; -1) ; B( -1 ; 5 ) ; C( 3 ; -3 )
a) Viết phương trình đường thẳng BC
b) Chứng minh 3 diểm A , B , C thẳng hàng
Giải đúng mk tick
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
4*. Cho ba điểm A(1;-2); B(-2; 4); C(-2,5 ; 5). Chứng tỏ rằng ba điểm A, B, C thẳng hàng.
mn ơi giúp mình với ![]()
\(\overrightarrow{AB}=\left(-3;6\right)\)
\(\overrightarrow{AC}=\left(-3,5;7\right)\)
Vì \(\overrightarrow{AB}=\dfrac{7}{6}\overrightarrow{AC}\)
nên A,B,C thẳng hàng
Cho ba điểm A(-1; 1), B(1;5), G(1 ; 2).
a) Chứng minh ba điểm A, B, G không thẳng hàng.
b) Tìm toạ độ điểm C sao cho G là trọng tâm của tam giác ABC.
a) Ta có: \(\overrightarrow {AB} = \left( {2;4} \right),\overrightarrow {AG} = \left( {2;1} \right)\)
Do \(\overrightarrow {AB} \ne k.\overrightarrow {AG} \) nên A, B, G không thẳng hàng
b) Giả sử C có tọa độ là: \(C\left( {{x_C};{y_C}} \right)\)
Để G là trọng tâm tam giác ABC thì: \(\left\{ \begin{array}{l}{x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3}\\{y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_C} = 3{x_G} - {x_A} - {x_B}\\{y_C} = 3{y_G} - {y_A} - {y_B}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_C} = 3.1 - \left( { - 1} \right) - 1 = 3\\{y_C} = 3.2 - 1 - 5 = 0\end{array} \right.\)
Vậy tọa độ điểm C là: \(C\left( {3;0} \right)\)
Cho ba điểm A,B,M , biết AM = 3,7 cm , MB = 2, 3 , AB = 5cm . Chứng tỏ rằng :
a , Trong ba điểm A , B , M không có điểm nào nằm giửa hai điểm còn lại
b, Ba điểm A, B ,M không thẳng hàng
Cho ba điểm A(3;5),B(-1;-7),C(2;-1). Chứng minh ba điểm A,B,C thẳng hàng
\(\overrightarrow{AB}=\left(-4;-12\right)\)
\(\overrightarrow{AC}=\left(-1;-6\right)\)
Vì -4/-1<>-12/-6
nên A,B,C ko thẳng hàng
Cho ba điểm A( 2;0), B ( 0; -2), C (3;1). Chứng tỏ rằng ba điểm A, B, C thẳng hàng.
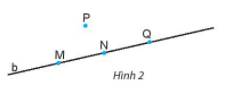
Trên Hình 2, hãy chỉ ra ba điểm thẳng hàng và ba điểm không thẳng hàng.
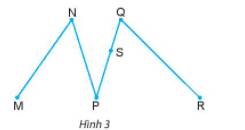
Dùng thước thẳng để kiểm tra xem ba điểm nào trên Hình 3 là thẳng hàng.
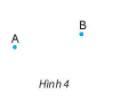
- Vẽ vào vở hai điểm A, B như Hình 4. Em vẽ thêm hai điểm C và D sao cho ba điểm A, B, C thẳng hàng và ba điểm A, B, D cũng thẳng hàng. Hãy vẽ ba vị trí khác nhau của điểm C.
- Trên Hình 2, ba điểm thẳng hàng là: M, N, Q; ba điểm không thẳng hàng là M, N, P
- Trên Hình 3, ba điểm thẳng hàng là M, P, R
- Vẽ hình như sau:
Cho ba điểm A(1; 2; 1), B(2; -1; 1), C(0; 3; 1) và đường thẳng d: x - 3 = y - 1 = z 2
Tìm tập hợp những điểm cách đều ba điểm A, B, C.
Gọi (Q) và (R) theo thứ tự là mặt phẳng trung trực của AB và BC.
Những điểm cách đều ba điểm A, B, C là giao tuyến ∆ = (Q) ∩ (R).
(Q) đi qua trung điểm E(3/2; 1/2; 1) của AB và có n Q → = AB→ (1; -3; 0) do đó phương trình của (Q) là: x - 3/2 - 3(y - 1/2) = 0 hay x - 3y = 0
(R) đi qua trung điểm F(1; 1; 1) của BC và có n R → = BC → = (-2; 4; 0) do đó phương trình (R) là: x - 2y + 1 = 0
Ta có: n Q → ∧ n R → = (0; 0; -2).
Lấy D(-3; -1; 0) thuộc (Q) ∩ (R)
Suy ra ∆ là đường thẳng đi qua D và có vectơ chỉ phương u → (0; 0; 1)
nên có phương trình là: 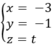
Cho ba điểm A(0; 1), B(1; 2), C(-5; -4).
a)Viết phương trình đường thẳng d đi qua hai điểm A và B.
b) Chứng minh ba điểm A, B, C thẳng hàng.
Lời giải:
a. Gọi ptdt $(d)$ đi qua $A,B$ là $y=ax+b$
Ta có: \(\left\{\begin{matrix} y_A=ax_A+b\\ y_B=ax_B+b\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 2=a+b\\ 1=a.0+b\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} b=1\\ a=1\end{matrix}\right.\)
Vậy ptđt $(d)$ là: $y=x+1$
b. Ta thấy: $y_C=-4=-5+1=x_C+1$ nên $C\in (d): y=x+1$
Tức là $C$ thuộc đt đi qua 2 điểm $A,B$
$\Rightarrow A,B,C$ thẳng hàng.
Cho đoạn thẳng MN = 6cm .Trên tia NM lấy điểm A sao cho NA = 3cm .
a)Trong ba điểm M,N,A điểm nào nằm giữa 2 điểm còn lại ? Tại sao?
b)Điểm A có là trung điểm của đoạn thẳng MN không ?Tại sao?
c)Ba đường thẳng MA,NA,MN có phải là ba đưởng thẳng phân biệt không?
Cho ba điểm A(1; 1), B(4;3) và C(0;- 2).
a) Chứng minh ba điểm A, B, C không thẳng hàng.
b) Tìm toạ độ điểm D sao cho tứ giác ABCD là hình thang có AB // CD và CD= 2AB.
a) Ta có: \(\overrightarrow {AB} = \left( {3;2} \right),\overrightarrow {AC} = \left( { - 1; - 3} \right)\)
Do \(\overrightarrow {AB} \ne k.\overrightarrow {AC} \) nên A, B, C không thẳng hàng
b) Giả sử tọa độ điểm D là:\(D\left( {{x_D},{y_D}} \right)\)
Ta có: \(\overrightarrow {CD} = \left( {{x_D} - 0;{y_D} - \left( { - 2} \right)} \right) = \left( {{x_D};{y_D} + 2} \right)\)
Để tứ giác ABCD là hình thang có AB // CD và CD= 2AB thì \(\overrightarrow {CD} = 2\overrightarrow {AB} \)
Vậy nên \(\overrightarrow {CD} = 2\overrightarrow {AB} \Leftrightarrow \left\{ \begin{array}{l}{x_D} = 2.3\\{y_D} + 2 = 2.2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_D} = 6\\{y_D} = 2\end{array} \right.\)
Vậy tọa độ D là: \(D\left( {6;2} \right)\)