Xét xem x0=-1 có phải nghiệm của pt (x+1)(x-2)(x-5)=0.
H24
Những câu hỏi liên quan
Xét xem x = -1 có là nghiệm của phương trình (x + 1)(x - 2)(x + 5) = 0 hay không?
Hướng dẫn giải:
Thay x = -1 vào phương trình
Ta được VT= (-1 + 1)(-1 – 2)(-1 + 5) = 0.(-3).4 = 0= VP
Vậy x = -1 là nghiệm của phương trình đã cho.
Đúng 0
Bình luận (0)
1. cho pt x2-2(m-2)x-2m0 với x là ẩn số giá trị của m để pt có 2 nghiệm là 2 số đối nhau là a,0 b, dfrac{-1}{2} c, 2 d, 4 2. biết rằng (x0; y0)là nghiệm của hệ pt left{{}begin{matrix}x+2y-302x-y-10end{matrix}right. tổng x0 + y0 bằng a,3 b,1 c,0 d, 23. trong △ABC vuông tại A có AC3; AB4 khi đó tanB bằng a,dfrac{4}{5} b,dfrac{3}{5} c,dfrac{3}{4} d dfrac{4}{3}4. trên đg tròn (O;R) lấy 2 điểm A,B sao cho số đo cung AB lớn hơn...
Đọc tiếp
1. cho pt x2-2(m-2)x-2m=0 với x là ẩn số giá trị của m để pt có 2 nghiệm là 2 số đối nhau là
a,0 b, \(\dfrac{-1}{2}\) c, 2 d, 4
2. biết rằng (x0; y0)là nghiệm của hệ pt \(\left\{{}\begin{matrix}x+2y-3=0\\2x-y-1=0\end{matrix}\right.\) tổng x0 + y0 bằng
a,3 b,1 c,0 d, 2
3. trong △ABC vuông tại A có AC=3; AB=4 khi đó tanB bằng
a,\(\dfrac{4}{5}\) b,\(\dfrac{3}{5}\) c,\(\dfrac{3}{4}\) d \(\dfrac{4}{3}\)
4. trên đg tròn (O;R) lấy 2 điểm A,B sao cho số đo cung AB lớn hơn bằng \(270^o\) độ dài dây cung là
a, R\(\sqrt{2}\) b, R\(\sqrt{3}\) c, R d, 2R\(\sqrt{2}\)
5. cho đg tròn (O;3cm) 2 điểm A,B thuộc đường tròn và sđ \(\stackrel\frown{AB}\) = \(60^o\) độ dài cung nhỏ AB là
a, \(\dfrac{\pi}{2}\) cm b, \(3\pi\) c, \(\dfrac{\pi}{3}cm\) d, \(\pi\)cm
6. giá trị của m để 2 đg thẳng (d): y=xm+6 và (d'): y=3x+2-m song song là
a, m=-2 b, m=-3 c, m=-4 d, m=1
7. cho hàm số bậc nhất y=ax+b có hệ số góc bằng -1 và tung độ góc bằng 3 giá trị của biểu thức a2+b bằng
a,2 b, 4 c, 9 d, 5
8. cho hệ pt \(\left\{{}\begin{matrix}3x+my=1\\nx+y=3\end{matrix}\right.\) với m,n là tham số biết rằng (x;y)=(1,1) là 1 nghiệm của hệ đã cho giá trị của m+n bằng
a, -1 b, 3 c, 1 d, 2
9.cho Parabol (P) có pt \(y=\dfrac{x^2}{4}\) vào đường thẳng (d): y=-2x-4
a, (P) cắt (d) tại 2 điểm phân biệt
b, (P) cắt (d) tại điểm duy nhất (-2;2)
c, (P) ko cắt (d)
d, (P) tiếp xúc với (d), tiếp điểm là (-4;4)
10. tất cả các giá trị của x để \(\sqrt{-2x+6}\) có nghĩa là
a, x≥3 b, x>3 c, x≤3 d, x<-3
Câu 3: C
Câu 4: A
Câu 5: C
Câu 6: m=3
Câu 7: B
Câu 8: D
Câu 9: D
Câu 10: C
Đúng 1
Bình luận (0)
Xét xem x = 2 có phải là nghiệm của phương trình: 3 - x = (x - 3)(1 - x) không?
(x-3)(1-x)=3-x
=>(x-3)(1-x)=-(x-3)
=>(x-3)(1-x+1)=0
=>(x-3)(2-x)=0
=>x=2 hoặc x=3
=>x=2 là nghiệm của pt
Đúng 1
Bình luận (1)
1, Xét pt x2 - m2x + 2m + 2 0 (ẩn x). Tìm số nguyên dương m để pt có nghiệm nguyên2,cho pt x3 + ax2 + bx - 1 0 a, tìm các số hữu tỉ a và b để pt có nghiệm x2-sqrt{3}b, Với a,b vừa tìm đc ở câu a, Gọi x1 ; x2 ; x3 là 3 nghiệm của pt trênTính Sfrac{1}{x_1^5}+frac{1}{x_2^5}+frac{1}{x_3^5}
Đọc tiếp
1, Xét pt x2 - m2x + 2m + 2 = 0 (ẩn x). Tìm số nguyên dương m để pt có nghiệm nguyên
2,cho pt x3 + ax2 + bx - 1 = 0
a, tìm các số hữu tỉ a và b để pt có nghiệm \(x=2-\sqrt{3}\)
b, Với a,b vừa tìm đc ở câu a, Gọi x1 ; x2 ; x3 là 3 nghiệm của pt trên
Tính \(S=\frac{1}{x_1^5}+\frac{1}{x_2^5}+\frac{1}{x_3^5}\)
Không biết câu 1 đề là m2x hay là mx ta ? Bởi nếu đề như vậy đenta sẽ là bậc 4 khó thành bình phương lắm
Làm câu 2 trước vậy , câu 1 để sau
a, pt có nghiệm \(x=2-\sqrt{3}\)
\(\Rightarrow pt:\left(2-\sqrt{3}\right)^3+a\left(2-\sqrt{3}\right)^2+b\left(2-\sqrt{3}\right)-1=0\)
\(\Leftrightarrow26-15\sqrt{3}+7a-4a\sqrt{3}+2b-b\sqrt{3}-1=0\)
\(\Leftrightarrow\sqrt{3}\left(4a+b+15\right)=7a+2b+25\)
Vì VP là số hữu tỉ
=> VT là số hữu tỉ
Mà \(\sqrt{3}\)là số vô tỉ
=> 4a + b + 15 = 0
=> 7a + 2b + 25 = 0
Ta có hệ \(\hept{\begin{cases}4a+b=-15\\7a+2b=-25\end{cases}}\)
Dễ giải được \(\hept{\begin{cases}a=-5\\b=5\end{cases}}\)
b, Với a = -5 ; b = 5 ta có pt:
\(x^3-5x^2+5x-1=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2-4x+1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=1\\x^2-4x+1=0\left(1\right)\end{cases}}\)
Giả sử x1 = 1 là 1 nghiệm của pt ban đầu
x2 ; x3 là 2 nghiệm của pt (1)
Theo Vi-ét \(\hept{\begin{cases}x_2+x_3=4\\x_2x_3=1\end{cases}}\)
Có: \(x_2^2+x_3^2=\left(x_2+x_3\right)^2-2x_2x_3=16-2=14\)
\(x_2^3+x_3^3=\left(x_2+x_3\right)\left(x^2_2-x_2x_3+x_3^2\right)=4\left(14-1\right)=52\)
\(\Rightarrow\left(x_2^2+x_3^2\right)\left(x_2^3+x_3^3\right)=728\)
\(\Leftrightarrow x_2^5+x_3^5+x_2^2x_3^2\left(x_2+x_3\right)=728\)
\(\Leftrightarrow x^5_2+x_3^5+4=728\)
\(\Leftrightarrow x_2^5+x_3^5=724\)
Có \(S=\frac{1}{x_1^5}+\frac{1}{x_2^5}+\frac{1}{x_3^5}\)
\(=1+\frac{x_2^5+x_3^5}{\left(x_2x_3\right)^5}\)
\(=1+724\)
\(=725\)
Vậy .........
Đúng 0
Bình luận (0)
Câu 1 đây , lừa người quá
Giả sử pt có 2 nghiệm x1 ; x2
Theo Vi-ét \(\hept{\begin{cases}x_1+x_2=m^2\\x_1x_2=2m+2\end{cases}}\)
\(Do\text{ }m\inℕ^∗\Rightarrow\hept{\begin{cases}S=m^2>0\\P=2m+2>0\end{cases}\Rightarrow}x_1;x_2>0\)
Lại có \(x_1+x_2=m^2\inℕ^∗\)
Mà x1 hoặc x2 nguyên
Nên suy ra \(x_1;x_2\inℕ^∗\)
Khi đó : \(\left(x_1-1\right)\left(x_2-1\right)\ge0\)
\(\Leftrightarrow x_1x_2-\left(x_1+x_2\right)+1\ge0\)
\(\Leftrightarrow2m+2-m^2+1\ge0\)
\(\Leftrightarrow-1\le m\le3\)
Mà \(m\inℕ^∗\Rightarrow m\in\left\{1;2;3\right\}\)
Thử lại thấy m = 3 thỏa mãn
Vậy m = 3
Đúng 0
Bình luận (0)
Xét xem xo có là nghiệm của phương trình hay không ?
a) x^2-3x+7=1+2x :xo=2
b) x^2-3x-10=0 ;xo=-2
c) x^2-3x+4=2(x-1) ;xo=2
d) (x+1)(x-2)(x-5)=0 ;xo=-1
e) 2x^2+3x+1=0 ;xo=-1
f) 4x^2-3x=2x-1 ;xo=5
Giúp e với ạ, với lại x^2 nghĩa là x mũ 2 ạ
- Thay lần lượt xo vào từng phương trình trên ta được kết quả sau :
+, Phương trình nhận xo là nghiệm : a, b, c, d, e .
Đúng 2
Bình luận (0)
Xét xem x = 3 5 có là nghiệm của phương trình (10x + 1)(3x + 2) – 5(x + 2) = 40
Hướng dẫn giải:
Thay 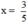 vào 2 vế của phương trình
vào 2 vế của phương trình
Ta được:
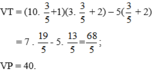
⇒ VT ≠ VP
Vậy 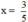 không là nghiệm của phương trình đã cho.
không là nghiệm của phương trình đã cho.
Đúng 0
Bình luận (0)
Hộ với nhanh nhacho pt (m-1)x2-2mx+m+10a,CM pt trên luôn có 2 nghiệm với mọi mb,Tìm các giá trị của m để pt có 2 nghiệm tích của 2 nghiệm 5.Từ đó hãy tính tổng 2 nghiệm của ptc, Tìm hệ thức liên hệ giữa 2 nghiệm của pt không phụ thuộc vào md,Tìm m để pt có 2 nghiệm x1 x2 thỏa mãn x1/x2+x2/x1+5/20
Đọc tiếp
Hộ với nhanh nha
cho pt (m-1)x2-2mx+m+1=0
a,CM pt trên luôn có 2 nghiệm với mọi m
b,Tìm các giá trị của m để pt có 2 nghiệm tích của 2 nghiệm =5.Từ đó hãy tính tổng 2 nghiệm của pt
c, Tìm hệ thức liên hệ giữa 2 nghiệm của pt không phụ thuộc vào m
d,Tìm m để pt có 2 nghiệm x1 x2 thỏa mãn x1/x2+x2/x1+5/2=0
1.a
ta có: \(\Delta'=m^2-\left(m-1\right)\left(m+1\right)\)
= m^2-m^2+1=1>0
vậy pt luôn có 2 no vs mọi m
Đúng 0
Bình luận (0)
a)\(\Delta=m^2-\left(m+1\right)\left(m-1\right)=m^2-m^2+1=1\)
Vậy pt luôn có 2 nghiệm với mọi m
b)
Theo hệ thức Vi ét ,ta có:
\(\hept{\begin{cases}x_1+x_2=\frac{2m}{m-1}\\x_1\cdot x_2=\frac{m+1}{m-1}=1+\frac{2}{m-1}\end{cases}}\)
mà \(\frac{m+1}{m-1}=5\Rightarrow m=1,5\)
vậy \(x_1\cdot x_2=\frac{2m}{m-1}=6\)
\(\hept{\begin{cases}x_1+x_2=\frac{2m}{m-1}=2+\frac{2}{m-1}\\x_1\cdot x_2=\frac{m+1}{m-1}=1+\frac{2}{m-1}\end{cases}}\)
\(\Rightarrow x_1+x_2-x_1\cdot x_2=2+\frac{2}{m-1}-1-\frac{2}{m-1}=1\)
c)
\(\frac{x_1}{x_2}+\frac{x_2}{x_1}+\frac{5}{2}=0\Rightarrow\frac{x_1^2+x_2^2+2x_1x_2+3x_1x_2}{2x_1x_2}=0\Rightarrow\left(x_1+x_2\right)^2+3x_1x_2=0\)
\(\Leftrightarrow\left(\frac{2m}{m-1}\right)^2+\frac{3\left(m+1\right)}{m-1}=0\Rightarrow m=\pm\sqrt{\frac{3}{7}}\)
Đúng 0
Bình luận (0)
Bài này t ra đề lâu lắm mà ko ai nghĩ ra ( sqrt[3]{23x^3+15x+8}+sqrt[5]{3x^5+19x-243}-x^{2n+1}-x^{2n-1}-x^{2n-3}-...-x-1 (1) Proposed by Pham Quang DuongGiải : Dễ thấy x 0 là 1 nghiệm của pt đã cho , ta đi c/m pt chỉ có 1 nghiệm duy nhất là x 0left(1right)Leftrightarrowsqrt[3]{23x^3+15x+8}+sqrt[5]{3x^5+19x-243}+x^{2n+1}+x^{2n-1}+...+x-1Xét hàm fleft(xright)VTXét 2 giá trị x1 ; x...
Đọc tiếp
Bài này t ra đề lâu lắm mà ko ai nghĩ ra =(
\(\sqrt[3]{23x^3+15x+8}+\sqrt[5]{3x^5+19x-243}=-x^{2n+1}-x^{2n-1}-x^{2n-3}-...-x-1\) (1)
Proposed by Pham Quang Duong
Giải : Dễ thấy x = 0 là 1 nghiệm của pt đã cho , ta đi c/m pt chỉ có 1 nghiệm duy nhất là x = 0
\(\left(1\right)\Leftrightarrow\sqrt[3]{23x^3+15x+8}+\sqrt[5]{3x^5+19x-243}+x^{2n+1}+x^{2n-1}+...+x=-1\)
Xét hàm \(f\left(x\right)=VT\)
Xét 2 giá trị x1 ; x2 của hàm trên
*Nếu x1 > x2 thì f(x1) > f(x2)
*Nếu x1 < x2 thì f(x1) < f(x2)
Do đó hàm f(x) mà ta xét đồng biến
=> pt chỉ có 1 nghiệm duy nhất x = 0
Vậy pt chỉ có 1 nghiệm đó là x = 0
Bài này lớp 11 mới đúng -,- nhưng dùng kiến thức lớp 7 để làm thôi
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
1, với giá trị nào của k thì pt x-ky-1 nhận cặp số (1;2) làm nghiệm?a, k2 b, k1 c, k-1 d, k02, cặp số (x0; y0) là nghiệm của hệ pt left{{}begin{matrix}x-y-2x1end{matrix}right. giá trị biểu thức x^2_0+y_0 bằng a, 4 b,5 c, 10 d, 73, hàm số y5x2 nghịch biến khi a, x0 b, x0 c, xinR ...
Đọc tiếp
1, với giá trị nào của k thì pt x-ky=-1 nhận cặp số (1;2) làm nghiệm?
a, k=2 b, k=1 c, k=-1 d, k=0
2, cặp số (x0; y0) là nghiệm của hệ pt \(\left\{{}\begin{matrix}x-y=-2\\x=1\end{matrix}\right.\) giá trị biểu thức \(x^2_0+y_0\) bằng
a, 4 b,5 c, 10 d, 7
3, hàm số y=5x2 nghịch biến khi
a, x>0 b, x<0 c, x\(\in\)R d, x≠0
4, tam giác ABC có 3 góc nhọn nội tiếp đường tròn tâm O biết sđ \(\stackrel\frown{AC}\)\(=80^o\) góc \(\widehat{ABC}\) có số đo là
a, 40o b, 80o c, 160o d, 140o
5, cho hàm số y= -2020x2 khẳng định nào sao đây ko đúng
a, hàm số nghịch biến khi x>0
b,đồ thị hàm số nằm ở phía dưới trục hoành
c, điểm O là điểm cao nhất của đồ thị
d, đồ thị hàm hố là một đường thẳng
6, cho hàm số y=f (x)=x2 giá trị của f(5) bằng
a, 10 b, -25 c, 25 d, -10
7, điểm M (-1;1) thuộc đồ thị hàm số y=(a-1)x2 khi a bằng
a, 2 b, 1 c, 0 d, -1
8, cho đường tròn tâm O bán kính 6m diện tích của đg tròn là
a, 36\(\pi\) (m2) b, 12\(\pi\) (m) c, 12\(\pi\) (m2) d, 36\(\pi\) (m)
9, phương trình nào sau đây có 2 nghiệm phân biệt
a, x2-x+1=0 b, x2-2x+1=0 c, x2-x-1=0 d, 25x2=0
10, pt 5x2-x-10=0 có toonge 2 nghiệm bằng
a, -1 b, 1 c, \(\dfrac{-1}{5}\) d, \(\dfrac{1}{5}\)
Câu 10: B
Câu 9: C
Câu 8: A
Câu 7: A
Câu 6: C
Câu 5:D
Câu 4: A
Câu 3: B
Câu 2: A
Câu 1; B
Đúng 2
Bình luận (0)




