Câu 22 23 24 với ạ
HP
Những câu hỏi liên quan
2+22+23+24+...+2100
ai giúp em với ạ
\(2\cdot A=2^2+2^3+...+2^{101}\)
\(\Leftrightarrow A=2^{101}-2\)
Đúng 0
Bình luận (0)
Đặt \(A=2+2^2+...+2^{100}\)
\(2A=2^2+2^3+...+2^{101}\\ 2A-A=\left(2^2+2^3+...+2^{101}\right)-\left(2+2^2+...+2^{100}\right)\\ A=2^{101}-2\)
Đúng 0
Bình luận (0)
Câu 22. Các đại diện của lớp giáp xác, các đặc điểm khác của chúng.
Câu 23. Vai trò của giáp xác.
Câu 24. Môi trường sống, hình dạng cấu tạo của nhện.
Câu 25. Tập tính của nhện.
mong giúp em với ạ ![]()
41+42+43+44-21-22-23-24=? Giúp em với ạ
41 + 42 + 43 + 44 - 21 - 22 - 23 - 24
= (41 - 21) + (42 - 22) + (43 - 23) + (44 - 24)
= 20 + 20 + 20 + 20
= 20 x 4
= 80
tk nha. chúc bn học giỏi :)
Đúng 0
Bình luận (0)
= 80 nha
TK MK NHA CÁC BẠN MK ĐG BỊ ÂM ĐIỂM
Đúng 0
Bình luận (0)
Giúp em thì ai giúp anh, chị đây! Hỏi mãi chưa có chế nào trả lời đây. Huhuhu$$$
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Câu 23, 24 và 25 ạ
Giải chi tiết ra giúp em với ạ

23.
Ta sẽ tìm điểm \(I\left(a;b;c\right)\) sao cho \(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=\overrightarrow{0}\) (1)
\(\left\{{}\begin{matrix}\overrightarrow{IA}=\left(-2-a;2-b;6-c\right)\\\overrightarrow{IB}=\left(-3-a;1-b;8-c\right)\\\overrightarrow{IC}=\left(-1-a;-b;7-c\right)\\\overrightarrow{ID}=\left(1-a;2-b;3-c\right)\end{matrix}\right.\)
\(\Rightarrow\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=\left(-5-4a;5-4b;24-4c\right)\)
(1) thỏa mãn khi: \(\left\{{}\begin{matrix}-5-4a=0\\5-4b=0\\24-4c=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-\dfrac{5}{4}\\b=\dfrac{5}{4}\\c=6\end{matrix}\right.\)
\(\Rightarrow I\left(-\dfrac{5}{4};\dfrac{5}{4};6\right)\)
Khi đó:
\(T=MA^2+MB^2+MC^2+MD^2=\left(\overrightarrow{MI}+\overrightarrow{IA}\right)^2+\left(\overrightarrow{MI}+\overrightarrow{IB}\right)^2+\left(\overrightarrow{MI}+\overrightarrow{IC}\right)^2+\left(\overrightarrow{MI}+\overrightarrow{ID}\right)^2\)
\(=4MI^2+IA^2+IB^2+IC^2+ID^2+2\overrightarrow{MI}\left(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}\right)\)
\(=4MI^2+IA^2+IB^2+IC^2+ID^2\) (do \(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=\overrightarrow{0}\))
\(IA^2+IB^2+IC^2+ID^2\) cố định nên \(T_{min}\) khi \(MI_{min}\)
\(\Leftrightarrow M\) trùng I
\(\Rightarrow M\left(-\dfrac{5}{4};\dfrac{5}{4};6\right)\Rightarrow x+y+z=-\dfrac{5}{4}+\dfrac{5}{4}+6=6\)
Đúng 1
Bình luận (0)
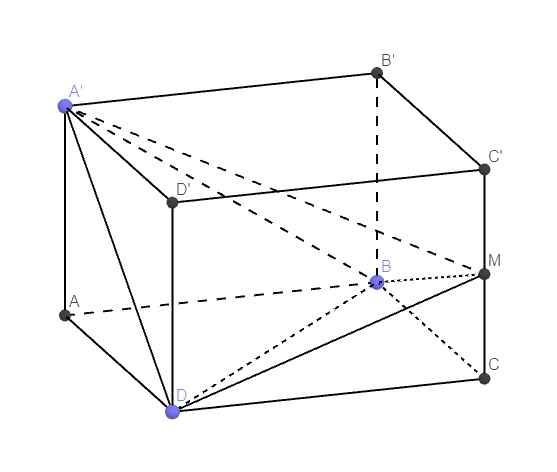
24.
\(a+b=4\Rightarrow b=4-a\)
ABCD là hình chữ nhật \(\Rightarrow\overrightarrow{AB}=\overrightarrow{DC}\)
\(\Rightarrow C\left(a;a;0\right)\)
Tương tự ta có: \(C'\left(a;a;b\right)\)
M là trung điểm CC' \(\Rightarrow M\left(a;a;\dfrac{b}{2}\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{A'B}=\left(a;0;-b\right)=\left(a;0;a-4\right)\\\overrightarrow{A'D}=\left(0;a;-b\right)=\left(0;a;a-4\right)\\\overrightarrow{A'M}=\left(a;a;-\dfrac{b}{2}\right)=\left(a;a;\dfrac{a-4}{2}\right)\end{matrix}\right.\)
Theo công thức tích có hướng:
\(\left[\overrightarrow{A'B};\overrightarrow{A'D}\right]=\left(-a^2+4a;-a^2+4a;a^2\right)\)
\(\Rightarrow V=\dfrac{1}{6}\left|\left[\overrightarrow{A'B};\overrightarrow{A'D}\right].\overrightarrow{A'M}\right|=\dfrac{1}{6}\left|a\left(-a^2+4a\right)+a\left(-a^2+4a\right)+\dfrac{a^2\left(a-4\right)}{2}\right|\)
\(=\dfrac{1}{4}\left|a^3-4a^2\right|=\dfrac{1}{4}\left(4a^2-a^3\right)\)
Xét hàm \(f\left(a\right)=\dfrac{1}{4}\left(4a^2-a^3\right)\) trên \(\left(0;4\right)\)
\(f'\left(a\right)=\dfrac{1}{4}\left(8a-3a^2\right)=0\Rightarrow\left[{}\begin{matrix}a=0\left(loại\right)\\a=\dfrac{8}{3}\end{matrix}\right.\)
\(\Rightarrow f\left(a\right)_{max}=f\left(\dfrac{8}{3}\right)=\dfrac{64}{27}\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
làm hộ mình câu 22 23 24
Câu 22:
TXĐ: $(-\infty;0]\cup [2;+\infty)$
BPT \(\Leftrightarrow \left\{\begin{matrix} x\geq -1\\ x^2-2x\leq (x+1)^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq -1\\ x\geq \frac{-1}{4}\end{matrix}\right.\Leftrightarrow x\geq \frac{-1}{4}\)
Kết hợp ĐKXĐ suy ra BPT có nghiệm $[\frac{-1}{4};0]\cup [2;+\infty)$
Đúng 1
Bình luận (0)
Câu 23:
Theo công thức trung tuyến:
$CM^2=\frac{BC^2+AC^2}{2}-\frac{AB^2}{4}=\frac{23}{2}$
Áp dụng công thức Herong cho tam giác $ABC$:
$S_{ABC}=\sqrt{\frac{9}{2}(\frac{9}{2}-2)(\frac{9}{2}-3)(\frac{9}{2}-4)}=\frac{3\sqrt{15}}{4}$
$S_{BCM}=\frac{1}{2}S_{ABC}=\frac{3\sqrt{15}}{8}$
Áp dụng công thức: $S=\frac{abc}{4R}$ cho tam giác $BCM$ thì bán kính đường tròn ngoại tiếp tam giác là:
$R=\frac{BC.CM.BM}{4S_{BCM}}=\frac{4.\sqrt{\frac{23}{2}}.1}{\frac{3\sqrt{15}}{2}}=\frac{4\sqrt{690}}{45}$
Đúng 0
Bình luận (0)
Câu 24:
Với $m=-1$ thì BPT $\Leftrightarrow -x-1<0\Leftrightarrow x>-1$ (chứ không phải với mọi $x\in\mathbb{R}$) (loại)
Với $m\neq -1$ thì để $(m+1)x^2+mx+m< 0$ với mọi $x\in\mathbb{R}$ thì:
\(\left\{\begin{matrix} m+1>0\\ \Delta=m^2-4m(m+1)< 0\end{matrix}\right.\Leftrightarrow m>0\)
Vậy $m\in (0;+\infty)$
Đúng 0
Bình luận (0)
Giải giúp mik câu này với ạ, mik cần gấp
So sánh: A=19^21+1/19^22+1 và B=19^22+1/19^23+1
bạn viết rõ lũy thừa giúp mình với
Đúng 0
Bình luận (0)
ý bạn là như này đk?
A=1921+1:1922+1
B=1922+1:1923+1
Đúng 0
Bình luận (0)
Xem thêm câu trả lời

 câu 21 22 23 24 giúp mình nha
câu 21 22 23 24 giúp mình nha
Mn giúp mình với ạ!Mình cảm ơn!!!
Bài 1:Chứng minh rằng B = 2 + 22 + 23 + 24 + ........ + 299 + 2100 chia hết cho 31.
Mình cảm ơn mn ạ!Giúp mình với tối nay 20:00 mình phải nộp bài rồi!!!
![]()
\(B=2+2^2+2^3+2^4+...+2^{99}+2^{100}=2\left(1+2^2+2^3+2^4\right)+...+2^{96}\left(1+2^2+2^3+2^4\right)=2.31+2^6.31+...+2^{96}.31=31\left(2+2^6+...+2^{96}\right)⋮31\)
Đúng 5
Bình luận (1)
B=2+22+23+24+...+299+2100=2(1+22+23+24)+...+296(1+22+23+24)=2.31+26.31+...+296.31=31(2+26+...+296)⋮31
Đúng 1
Bình luận (0)
câu 21 câu 22 câu 23 cau 24 câu 25 câu 26 câu 27 câu 28 câu 29 câu 30
Đọc tiếp
câu 21
câu 22
câu 23
cau 24
câu 25
câu 26
câu 27
câu 28
câu 29
câu 30
Câu 21: B
Câu 22: A
Câu 23: C
Câu 24: B
Câu 25: D
Câu 26: A
Câu 27: C
Câu 28: B
Câu 29: B
Câu 30: B
Đúng 0
Bình luận (0)