23.
Ta sẽ tìm điểm \(I\left(a;b;c\right)\) sao cho \(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=\overrightarrow{0}\) (1)
\(\left\{{}\begin{matrix}\overrightarrow{IA}=\left(-2-a;2-b;6-c\right)\\\overrightarrow{IB}=\left(-3-a;1-b;8-c\right)\\\overrightarrow{IC}=\left(-1-a;-b;7-c\right)\\\overrightarrow{ID}=\left(1-a;2-b;3-c\right)\end{matrix}\right.\)
\(\Rightarrow\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=\left(-5-4a;5-4b;24-4c\right)\)
(1) thỏa mãn khi: \(\left\{{}\begin{matrix}-5-4a=0\\5-4b=0\\24-4c=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-\dfrac{5}{4}\\b=\dfrac{5}{4}\\c=6\end{matrix}\right.\)
\(\Rightarrow I\left(-\dfrac{5}{4};\dfrac{5}{4};6\right)\)
Khi đó:
\(T=MA^2+MB^2+MC^2+MD^2=\left(\overrightarrow{MI}+\overrightarrow{IA}\right)^2+\left(\overrightarrow{MI}+\overrightarrow{IB}\right)^2+\left(\overrightarrow{MI}+\overrightarrow{IC}\right)^2+\left(\overrightarrow{MI}+\overrightarrow{ID}\right)^2\)
\(=4MI^2+IA^2+IB^2+IC^2+ID^2+2\overrightarrow{MI}\left(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}\right)\)
\(=4MI^2+IA^2+IB^2+IC^2+ID^2\) (do \(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=\overrightarrow{0}\))
\(IA^2+IB^2+IC^2+ID^2\) cố định nên \(T_{min}\) khi \(MI_{min}\)
\(\Leftrightarrow M\) trùng I
\(\Rightarrow M\left(-\dfrac{5}{4};\dfrac{5}{4};6\right)\Rightarrow x+y+z=-\dfrac{5}{4}+\dfrac{5}{4}+6=6\)
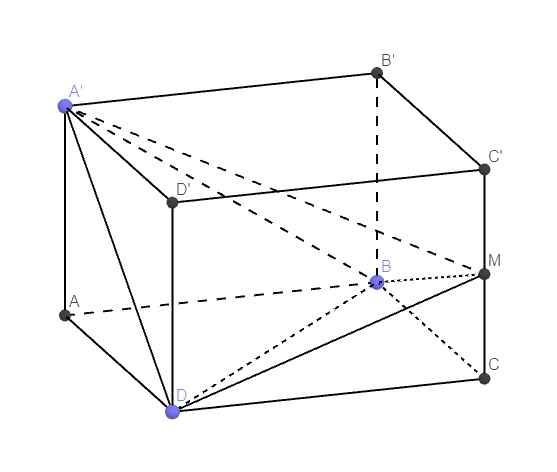
24.
\(a+b=4\Rightarrow b=4-a\)
ABCD là hình chữ nhật \(\Rightarrow\overrightarrow{AB}=\overrightarrow{DC}\)
\(\Rightarrow C\left(a;a;0\right)\)
Tương tự ta có: \(C'\left(a;a;b\right)\)
M là trung điểm CC' \(\Rightarrow M\left(a;a;\dfrac{b}{2}\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{A'B}=\left(a;0;-b\right)=\left(a;0;a-4\right)\\\overrightarrow{A'D}=\left(0;a;-b\right)=\left(0;a;a-4\right)\\\overrightarrow{A'M}=\left(a;a;-\dfrac{b}{2}\right)=\left(a;a;\dfrac{a-4}{2}\right)\end{matrix}\right.\)
Theo công thức tích có hướng:
\(\left[\overrightarrow{A'B};\overrightarrow{A'D}\right]=\left(-a^2+4a;-a^2+4a;a^2\right)\)
\(\Rightarrow V=\dfrac{1}{6}\left|\left[\overrightarrow{A'B};\overrightarrow{A'D}\right].\overrightarrow{A'M}\right|=\dfrac{1}{6}\left|a\left(-a^2+4a\right)+a\left(-a^2+4a\right)+\dfrac{a^2\left(a-4\right)}{2}\right|\)
\(=\dfrac{1}{4}\left|a^3-4a^2\right|=\dfrac{1}{4}\left(4a^2-a^3\right)\)
Xét hàm \(f\left(a\right)=\dfrac{1}{4}\left(4a^2-a^3\right)\) trên \(\left(0;4\right)\)
\(f'\left(a\right)=\dfrac{1}{4}\left(8a-3a^2\right)=0\Rightarrow\left[{}\begin{matrix}a=0\left(loại\right)\\a=\dfrac{8}{3}\end{matrix}\right.\)
\(\Rightarrow f\left(a\right)_{max}=f\left(\dfrac{8}{3}\right)=\dfrac{64}{27}\)
25.
H là trung điểm CD \(\Rightarrow H\left(0;1;5\right)\)
\(\left\{{}\begin{matrix}\overrightarrow{AB}=\left(-1;-1;2\right)\\\overrightarrow{AD}=\left(3;0;-3\right)\end{matrix}\right.\)\(\Rightarrow\left[\overrightarrow{AB};\overrightarrow{AD}\right]=\left(3;3;3\right)\) \(\Rightarrow S_{ABD}=\dfrac{1}{2}\left|\left[\overrightarrow{AB};\overrightarrow{AD}\right]\right|=\dfrac{3\sqrt{3}}{2}\)
\(\left\{{}\begin{matrix}\overrightarrow{CB}=\left(-2;1;1\right)\\\overrightarrow{CD}=\left(2;2;-4\right)\end{matrix}\right.\) \(\Rightarrow\left[\overrightarrow{CB};\overrightarrow{CD}\right]=\left(-6;-6;-6\right)\)\(\Rightarrow S_{BCD}=\dfrac{1}{2}\left|\left[\overrightarrow{CB};\overrightarrow{CD}\right]\right|=3\sqrt{3}\)
\(\Rightarrow S_{ABCD}=\dfrac{3\sqrt{3}}{2}+3\sqrt{3}=\dfrac{9\sqrt{3}}{2}\)
\(\Rightarrow V=\dfrac{1}{3}SH.S_{ABCD}=\dfrac{1}{3}.SH.\dfrac{9\sqrt{3}}{2}=\dfrac{27}{2}\)
\(\Rightarrow SH=3\sqrt{3}\)
\(\left[\overrightarrow{AB};\overrightarrow{AD}\right]=\left(3;3;3\right)=3\left(1;1;1\right)\Rightarrow\) mặt phẳng (ABCD) nhận \(\left(1;1;1\right)\) là 1 vtpt
SH vuông góc ABCD \(\Rightarrow\) \(\overrightarrow{SH}\) có dạng \(k\left(1;1;1\right)=\left(k;k;k\right)\)
\(\Rightarrow SH=\left|k\right|\sqrt{3}\)
\(\Rightarrow\left|k\right|\sqrt{3}=3\sqrt{3}\Rightarrow\left[{}\begin{matrix}k=3\\k=-3\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\overrightarrow{SH}=\left(3;3;3\right)\\\overrightarrow{SH}=\left(-3;-3;-3\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}S_1\left(-3;-2;2\right)\\S_2\left(3;4;8\right)\end{matrix}\right.\) \(\Rightarrow I\left(0;1;5\right)\)
Cả 4 đáp án đều sai
Tính đi tính lại mấy lần tưởng mình sai, đến lúc sử dụng phần mềm geogebra kiểm tra lại thì đáp án của bài toán sai.