NÓNG: LỊCH THI VÀ ĐỀ THI MINH HỌA TỐT NGHIỆP THPT NĂM 2023 - CHÍNH THỨC
*Link bài đăng Facebook: https://www.facebook.com/vice.contest/posts/pfbid0rUAgHyVScfeBnyLtdDXTsMgJNxn7yqbmskfTgftCFSR88hXt7HTR7CgAGdqFqCEVl
---------------------------------
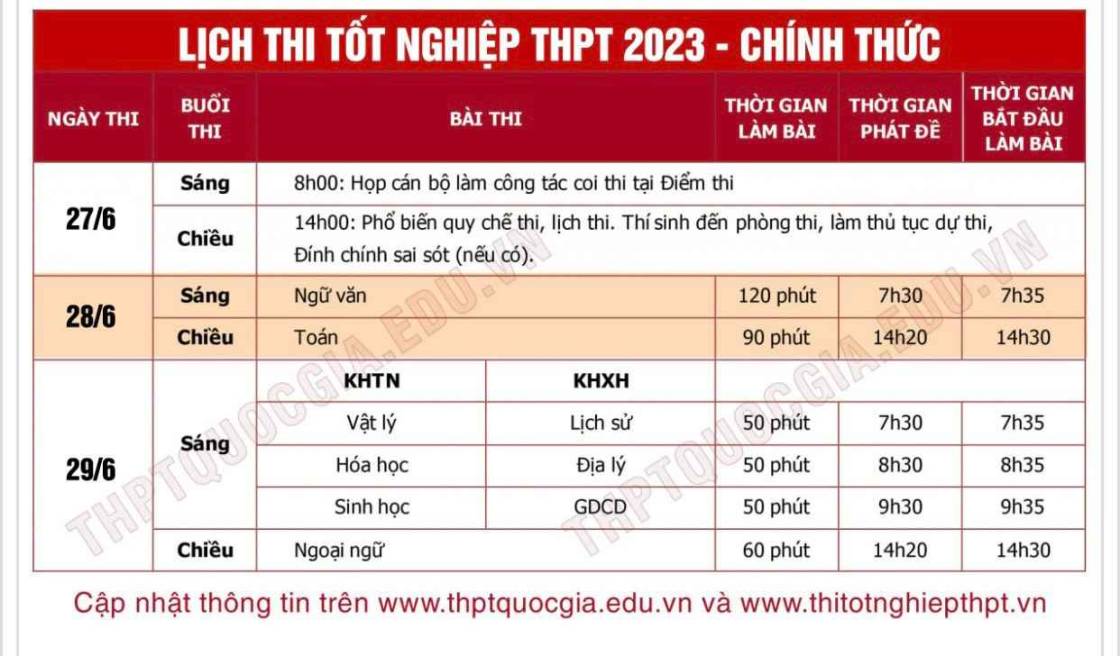
Cuộc thi Trí tuệ VICE xin gửi đến tất cả các followers 2k5 lộ trình thi tốt nghiệp Trung học phổ thông vừa được thống nhất và công bố bởi Bộ GD-ĐT vào sáng ngày 1/3. Ngoài ra, dưới đây là 15 đề thi minh họa được Bộ công bố trong văn bản cùng tên.
Link 15 đề thi minh họa:
1. Toán: https://drive.google.com/file/d/1jNO-Nj9ny6fJr-XYaTns7br6lPeQFPsi/view
2. Ngữ văn: https://drive.google.com/file/d/1Bql3jlQsGMhsrcnl_Rn9n0kBgpbYSipa/view
3. Vật lí: https://drive.google.com/file/d/1Uq2oebwZUUFSoORiS9YwnNPHYsbwCO-o/view
4. Hóa học: https://drive.google.com/file/d/1bJo5a39LuqI_VQ4Svy5lSLmh4iinge0v/view
5. Sinh học: https://drive.google.com/file/d/1Oi73NacwWyRuyJCmE0oEeOvDF6xkqeC3/view
6. Lịch sử: https://drive.google.com/file/d/1t4nTIc58PXAxi5Tl9rwswpUvrMFue5Bw/view
7. Địa lí: https://drive.google.com/file/d/1ZYTsgoTZO6_psIAXQlMWsGTOoi1J20cD/view
8. Giáo dục công dân: https://drive.google.com/file/d/1xtlii0CsrztBhyllSXZtWEYFoZaFJ1Yg/view
9. Tiếng Anh: https://drive.google.com/file/d/1a5p3uKx4-mqYB1CQsTqS7CPNtWP0HCCS/view
10. Tiếng Nga: https://drive.google.com/file/d/1JR-AZqhL_iBo517O3my9Q7pjHw2B9qzM/view
11. Tiếng Pháp: https://drive.google.com/file/d/15JW_6t2AqEfV_GZg_QWUoEocZtbcX5Uh/view
12. Tiếng Trung Quốc: https://drive.google.com/file/d/1rdixUT0aZlTam2jwWB09TVM-s2_O0a5l/view
13. Tiếng Đức: https://drive.google.com/file/d/1sgSS6FHXaZTGZoMTI1hxpHKmb7EW8LwL/view
14. Tiếng Nhật: https://drive.google.com/file/d/1Qv-onE0FRiJxjnDARfnfquO_GoA7nH5q/view
15. Tiếng Hàn: https://drive.google.com/file/d/1GvM4JtW1txV0ZO96XV_UyNB20CMn4JE9/view
Ngoài ra, theo lịch thi tốt nghiệp THPT, thí sinh sẽ có mặt vào chiều ngày 27/6/2023 để được phổ biến quy chế thi, và làm bài thi Toán - Văn - Tổ hợp khoa học - Ngoại ngữ trong 2 ngày 28/6 và 29/6. Năm nay, Bộ GD-ĐT đã đẩy sớm lịch thi tốt nghiệp lên nửa tháng.
Hãy theo dõi chúng mình để có những tin tức mới nhất về kì thi THPT, kì thi vào 10 và chứng chỉ ngoại ngữ IELTS nhé!