tính nguyên hàm của hàm số:
\(I=\int\frac{1+sinx}{1+cosx}dx\)
TC
Những câu hỏi liên quan
H24
5 tháng 3 2022 lúc 10:20
Tính nguyên hàm các hàm số sau:
1. \(I=\int\dfrac{cos^2x}{sin^8x}dx\)
2. \(I=\int\left(e^{sinx}+cosx\right)cosxdx\)
1.
\(I=\int\dfrac{cot^2x}{sin^6x}dx=\int\dfrac{cot^2x}{sin^4x}.\dfrac{1}{sin^2x}=\int cot^2x\left(1+cot^2x\right)^2.\dfrac{1}{sin^2x}dx\)
Đặt \(u=cotx\Rightarrow du=-\dfrac{1}{sin^2x}dx\)
\(I=-\int u^2\left(1+u^2\right)^2du=-\int\left(u^6+2u^4+u^2\right)du\)
\(=-\dfrac{1}{7}u^7+\dfrac{2}{5}u^5+\dfrac{1}{3}u^3+C\)
\(=-\dfrac{1}{7}cot^7x+\dfrac{2}{5}cot^5x+\dfrac{1}{3}cot^3x+C\)
Đúng 1
Bình luận (0)
2.
\(I=\int\left(e^{sinx}+cosx\right).cosxdx=\int e^{sinx}.cosxdx+\int cos^2xdx\)
\(=\int e^{sinx}.d\left(sinx\right)+\dfrac{1}{2}\int\left(1+cos2x\right)dx\)
\(=e^{sinx}+\dfrac{1}{2}x+\dfrac{1}{4}sin2x+C\)
Đúng 1
Bình luận (0)
tính nguyên hàm\(\int\frac{sinx}{9-cos^2x}dx\)
\(\int\dfrac{\sin x}{9-\cos^2x}dx=\int\dfrac{\sin x}{(3- \cos x)(3+\cos x)}dx\)
\(=-\int\dfrac{1}{(3- \cos x)(3+\cos x)}d(\cos x)\)
\(=\dfrac{-1}{6}.\int[\dfrac{1}{(3- \cos x)}+\dfrac{1}{(3+ \cos x)}]d(\cos x)\)
\(=\dfrac{1}{6}.\int\dfrac{d(3-\cos x)}{(3- \cos x)}-\dfrac{1}{6}.\int\dfrac{d(3+\cos x)}{(3+ \cos x)}\)
\(=\dfrac{1}{6}.\ln\dfrac{3-\cos x}{3+\cos x}\)
Đúng 0
Bình luận (0)
Tìm nguyên hàm của hàm số f(x)=\(\int\dfrac{sinx+2cosx}{3cosx+sinx}dx\) bằng phương pháp đổi biến , giúp mình với ạ
TD
7 tháng 10 2021 lúc 21:36
Nguyên hàm từ 0 đến pi/6 của (1-sin2x+cos2x)/(sinx-cosx)dx
Cho hàm
f
:
0
;
π
2
→
R
là hàm liên tục thỏa mãn
∫
0
π
2
f
(
x
)
2...
Đọc tiếp
Cho hàm f : 0 ; π 2 → R là hàm liên tục thỏa mãn
∫ 0 π 2 f ( x ) 2 - 2 f ( x ) ( sin x - cos x ) d x = 1 - π 2
Tính ∫ 0 π 2 f ( x ) d x .
A. ∫ 0 π 2 f ( x ) d x = - 1 .
B. ∫ 0 π 2 f ( x ) d x = 0
C. ∫ 0 π 2 f ( x ) d x = 2 .
D. ∫ 0 π 2 f ( x ) d x = 1 .
Cho hàm
f
:
[
0
;
π
2
]
→
R
là hàm liên tục thỏa mãn
∫
0
π
2
[
f
(
x
)
]
2
-
2
f
(
x
)
(
sin...
Đọc tiếp
Cho hàm f : [ 0 ; π 2 ] → R là hàm liên tục thỏa mãn ∫ 0 π 2 [ f ( x ) ] 2 - 2 f ( x ) ( sin x - cos x ) ] d x = 1 - π 2 . Tính ∫ 0 π 2 f ( x ) d x .
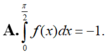
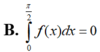
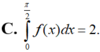
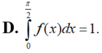
Tìm nguyên hàm:
\(\int\dfrac{sin2x}{\left(2+sinx\right)^2}dx\)
Tìm nguyên hàm của các hàm số sau:
a) \(\int\left(6x-\dfrac{1}{sin^2x}+1\right)dx\)
b) \(\int\dfrac{x^3+2x^2-1}{x^2}dx\)
Tìm nguyên hàm các hàm số hữu tỉ sau :
a.) \(\int\frac{1}{x^2-3x+2}dx\)
b) \(\int\frac{1}{4x^2-3x-1}dx\)
a) \(\int\frac{1}{x^2-3x+2}dx=\frac{1}{2-1}\int\frac{1}{\left(x-1\right)\left(x-2\right)}dx\)
=\(\int\frac{1}{x-2}dx-\int\frac{1}{x-1}dx=ln\left|x-2\right|-ln\left|x-1\right|=ln\left|\frac{x-2}{x-1}+C\right|\)
b) \(\int\frac{1}{4x^2-3x-1}dx=\frac{1}{4}.\frac{1}{\left(1-\frac{1}{4}\right)}\int\frac{1}{\left(x+\frac{1}{4}\right)\left(x-1\right)}dx\)
=\(\frac{1}{3}.\left[\int\frac{1}{x-1}dx-\int\frac{1}{x+\frac{1}{4}}dx\right]\)
=\(\frac{1}{3}\left[ln\left|x-1\right|-ln\left|x+\frac{1}{4}\right|\right]=\frac{1}{3}ln\left|\frac{x-1}{x+\frac{1}{4}}\right|+C\)
=\(\frac{1}{3}ln\left|\frac{4\left(x-1\right)}{4x+1}+C\right|\)
Đúng 0
Bình luận (0)