Giải phương trình:
(x2+5x)2+2x2+10x=24
Giải phương trình sau bằng cách đặt ẩn phụ
a) x 2 − 5 x + 5 = − 2 x 2 + 10 x − 11 .
b) 3 x 2 + 3 x = x + 5 2 − x + 6 .
giải phương trình : 2x2-5\(\sqrt{x^2_{ }-5x+7}\) =10x-17
2\(x^2\) - 5 \(\sqrt{x^2-5x+7}\) = 10\(x\) - 17 Đk \(x^2\) - 5\(x\) + 7 ≥ 0
\(x^2\) - 2.\(\dfrac{5}{2}\)\(x\) + \(\dfrac{25}{4}\) + \(\dfrac{3}{4}\) = (\(x\) - \(\dfrac{5}{2}\))2 + \(\dfrac{3}{4}\) > 0 ∀ \(x\)
ta có: 2\(x^2\) - 5\(\sqrt{x^2-5x+7}\) = 10\(x\) - 17
2\(x^2\) - 5\(\sqrt{x^2-5x+7}\) - 10\(x\) + 17 = 0
(2\(x^2\) - 10\(x\) + 14) - 5\(\sqrt{x^2-5x+7}\) + 3 = 0
2.(\(x^2\) - 5\(x\) + 7) - 5.\(\sqrt{x^2-5x+7}\) + 3 = 0
Đặt \(\sqrt{x^2-5x+7}\) = y > 0 ta có:
2y2 - 5y + 3 = 0
2 + (-5) + 3 = 0
⇒ y1= 1; y2 = \(\dfrac{3}{2}\)
TH1 y = 1 ⇒ \(\sqrt{x^2-5x+7}\) = 1
⇒ \(x^2\) - 5\(x\) + 7 = 1
\(x^2\) - 5\(x\) + 6 = 0
\(\Delta\) = 25 - 24 = 49
\(x_1\) = \(\dfrac{-\left(-5\right)+\sqrt{1}}{2}\) = 3;
\(x_2\) = \(\dfrac{-\left(-5\right)-\sqrt{1}}{2}\) = 2;
TH2 y = \(\dfrac{3}{2}\)
\(\sqrt{x^2-5x+7}\) = \(\dfrac{3}{2}\)
\(x^2\) - 5\(x\) + 7 = \(\dfrac{9}{4}\)
4\(x^2\) - 20\(x\) + 28 = 9
4\(x^2\) - 20\(x\) + 19 = 0
\(\Delta'\) = 102 - 4.19
\(\Delta'\) = 24
\(x_1\) = \(\dfrac{-\left(-10\right)+\sqrt{24}}{4}\) = \(\dfrac{10+\sqrt{24}}{4}\)
\(x_2\) = \(\dfrac{-\left(-10\right)-\sqrt{24}}{4}\) = \(\dfrac{10-\sqrt{24}}{4}\)
8 - 5\(\sqrt{6}\)
Từ các lập luận trên kết luận phương trình có tập nghiệm là:
S = {8 - 5\(\sqrt{6}\); 2 ; 3; 8 + 5\(\sqrt{6}\)}
2 - 5 = 10 - 17 Đk - 5 + 7 ≥ 0
- 2. + + = ( - )2 + > 0 ∀
ta có: 2 - 5 = 10 - 17
2 - 5 - 10 + 17 = 0
(2 - 10 + 14) - 5 + 3 = 0
2.( - 5
Để phương trình sau có 4 nghiệm phân biệt: 10 x − 2 x 2 − 8 = x 2 − 5 x + a . Giá trị của tham số a là:
A. a ∈ 1 ; 10
B. a = 1
C. 4 < a < 43 4
D. a ∈ 4 ; 45 4
Phương trình đã cho tương đương:
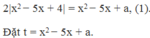
Phương trình (1) trở thành: 2 t + 4 - a = t 2
Phương trình (2) ⇔ t ≥ 0 t = 2 a − 8 t = 2 a − 8 3 để phương trình (1) có 4 nghiệm phân biệt thì điều kiện cần là (2) phải có 2 nghiệm phân biệt, tức là 2 a − 8 > 0 ⇔ a > 4 *
Khi đó, thay lại ta có: x 2 − 5 x + a = 2 a − 8 3 x 2 − 15 x + 3 a = 2 a − 8 ⇔ x 2 − 5 x + 8 − a = 0 ( 3 ) 3 x 2 − 15 x + a + 8 = 0 ( 4 )
Điều kiện để (1) có 4 nghiệm phân biệt là mỗi phương trình bậc 2 ở trên có 2 phân biệt và 2 nghiệm của (3) không thỏa mãn (4)
Mỗi phương trình (3), (4) có hai nghiệm phân biệt khi và chỉ khi
Δ 1 = 25 − 4 8 − a > 0 Δ 2 = 15 2 − 4.3 a + 8 > 0 ⇔ a > 7 4 a < 43 4 ⇔ 7 4 < a < 43 4
Nếu x là nghiệm của (3) thì không thỏa mãn (4)
⇒ x 2 − 5 x + 8 − a = 0 3 x 2 − 15 x + a + 8 ≠ 0 ⇒ x 2 − 5 x + 8 − a = 0 3 x 2 − 5 x + 8 − a − 16 + 4 a ≠ 0
⇒ 4 a − 16 ≠ 0 ⇔ a ≠ 4
So với điều kiện (*), suy ra 4 < a < 43 4
Đáp án cần chọn là: C
giải phương trình (x2+4x+8)(x2+5x+8)=2x2
\(\left(x^2+4x+8\right)\left(x^2+5x+8\right)=2x^2\left(1\right)\)
\(\Leftrightarrow x^4+5x^3+8x^2+4x^3+20x^2+32x+8x^2+40x+64-2x^2=0\)
\(\Leftrightarrow x^4+5x^3+4x^3+8x^2+20x^2+8x^2-2x^2+40x+32x+64=0\)
\(\Leftrightarrow x^4+9x^3+34x^2+72x+64=0\)
\(\Leftrightarrow x^4+2x^3+7x^3+14x^2+20x^2+40x+32x+64=0\)
\(\Leftrightarrow x^3\left(x+2\right)+7x^2\left(x+2\right)+20x\left(x+2\right)+32\left(x+2\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(x^3+7x^2+20x+32\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(x^3+4x^2+3x^2+12x+8x+32\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left[x^2\left(x+4\right)+3x\left(x+4\right)+8\left(x+4\right)\right]=0\)
\(\Leftrightarrow\left(x+2\right)\left(x+4\right)\left(x^2+3x+8\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+2=0\\x+4=0\\x^2+3x+8=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=-4\\vô.nghiệm\left(\Delta=9-32=-23< 0\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=-4\end{matrix}\right.\) là nghiệm của phương trình \(\left(1\right)\)
`4x=2+xx+1x<=>4x=2+3x<=>4x-3x=2<=>1x=2<=>x=2`
Giúp vs ạ
Bài 1 giải các bất phương trình sau
a.x2 - x - 6 = 0
b.2x2 - 7x + 5 < 0
c.3x2 - 9x + 6 ≥ 0
d.2x2 - 5x + 3 < 0
Bài 2 Giải phương trình sau
A.√x2 + x + 5 = √2x2 - 4x + 1
B.√11x2 -14x - 12 = √3x2 + 4x - 7
Bài 2:
a: =>2x^2-4x+1=x^2+x+5
=>x^2-5x-4=0
=>\(x=\dfrac{5\pm\sqrt{41}}{2}\)
b: =>11x^2-14x-12=3x^2+4x-7
=>8x^2-18x-5=0
=>x=5/2 hoặc x=-1/4
gọi x1,x2 là 2 nghiệm của phương trình \(3x^2+5X-6=0\) không giải phương trình hãy lập phương trình bậc hai ẩn y có 2 nghiệm y1,y2 thỏa mãn y1=2x1-x2 và y2=2x2-x1
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{5}{3}\\x_1x_2=-2\end{matrix}\right.\)
Ta có: \(\left\{{}\begin{matrix}y_1+y_2=2x_1-x_2+2x_2-x_1\\y_1y_2=\left(2x_1-x_2\right)\left(2x_2-x_1\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}y_1+y_2=x_1+x_2\\y_1y_2=-2x_1^2-2x_2^2+5x_1x_2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}y_1+y_2=-\dfrac{5}{3}\\y_1y_2=-2\left(x_1+x_2\right)^2+9x_1x_2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}y_1+y_2=-\dfrac{5}{3}\\y_1y_2=-2.\left(-\dfrac{5}{3}\right)^2+9.\left(-2\right)=-\dfrac{212}{9}\end{matrix}\right.\)
\(\Rightarrow y_1;y_2\) là nghiệm của:
\(y^2+\dfrac{5}{3}y-\dfrac{212}{9}=0\Leftrightarrow9y^2+10y-212=0\)
Giải các bất phương trình: 5 x - 20 3 - 2 x 2 + x 2 > x 1 - 3 x 3 - 5 x 4
Ta có:
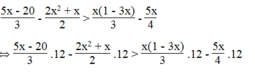
⇔ 20x – 80 – 12 x 2 – 6x > 4x – 12 x 2 – 15x
⇔ 20x – 12 x 2 – 6x – 4x + 12x2 + 15x > 80
⇔ 25x > 80
⇔ x > 3,2
Vậy tập nghiệm của bất phương trình là {x|x > 3,2}
Giải phương trình :
1) √x2+x+2 + 1/x= 13-7x/2
2) x2 + 3x = √1-x + 1/4
3) ( x+3)√48-x2-8x= 28-x/ x+3
4) √-x2-2x +48= 28-x/x+3
5) 3x2 + 2(x-1)√2x2-3x +1= 5x + 2
6) 4x2 +(8x - 4)√x -1 = 3x+2√2x2 +5x-3
7) x3/ √16-x2 + x2 -16 = 0
Giải phương trình chứa ẩn ở mẫu:
a. (x+1)/(x-2) - (x-1)(x+2) = 2(x2 + 2)/(x2 - 4)
b. (2x+1)/(x-1) = 5(x-1)/(x+1)
c. (x-1)/(x+2) - (x)/(x-2) = (5x-2)/(4 - x2)
d. (x-2)/(2+x)-(3)/(x-2)= 2(x-11)/(x2 - 2)
e. (x-1)/(x+1)-(x2 + x - 2)/(x+1)= (x+1)/(x-1) - x - 2
f. (x+1)/(x-1)-(x-1)/(x+1)=(4)/(x2 - 1)
g. (3)/4(x-5) + (15)/(50-2x2)= - (7)/6(x+5)
h. (12)/(8+x3)= 1 + (1)/(x+2)
k. (x+25)/(2x2 - 50)-(x+5)(x2 - 5x)= (5-x)(2x2 + 10x)
\(a,\frac{x+1}{x-2}-\frac{x-1}{x+2}=\frac{2\left(x^2+2\right)}{x^2-4}\)
\(\Leftrightarrow\frac{\left(x+1\right)\left(x+2\right)}{\left(x+2\right)\left(x-2\right)}-\frac{\left(x-1\right)\left(x-2\right)}{\left(x+2\right)\left(x-2\right)}=\frac{2x^2+4}{\left(x-2\right)\left(x+2\right)}\)
\(\Rightarrow x^2+2x+x+2-\left(x^2-2x-x+2\right)=2x^2+4\)
\(\Leftrightarrow x^2+3x+2-x^2+2x+x-2=2x^2+4\)
\(\Leftrightarrow6x=2x^2+4\)
\(\Leftrightarrow2x^2+4-6x=0\)
\(\Leftrightarrow2x^2+4-6x=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+3\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-1=0\\x+3=0\end{cases}\Leftrightarrow}\orbr{\begin{cases}x=1\\x=-3\end{cases}}\)
\(b,\frac{2x+1}{x-1}=\frac{5\left(x-1\right)}{x+1}\)
\(\Leftrightarrow\left(2x+1\right)\left(x+1\right)=5\left(x-1\right)\left(x-1\right)\)
\(\Leftrightarrow2x^2+2x+x+1=5\left(x^2-2x+1\right)\)
\(\Leftrightarrow2x^2+3x+1=5x^2-10x+5\)
\(\Leftrightarrow5x^2-2x^2-10x-3x+5-1=0\)
\(\Leftrightarrow3x^2-13x+4=0\)
\(\Leftrightarrow\left(x-4\right)\left(x-\frac{1}{3}\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-4=0\\x-\frac{1}{3}=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=4\\x=\frac{1}{3}\end{cases}}}\)
\(c,\frac{x-1}{x+2}-\frac{x}{x-2}=\frac{5x-2}{4-x^2}\)
\(\Leftrightarrow\frac{x-1}{x+2}-\frac{x}{x-2}=\frac{2-5x}{x^2-4}\)
\(\Leftrightarrow\frac{\left(x-1\right)\left(x-2\right)}{\left(x+2\right)\left(x-2\right)}-\frac{x\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}=\frac{2-5x}{\left(x-2\right)\left(x+2\right)}\)
\(\Rightarrow x^2-2x-x+2-x^2-2x=2-5x\)
\(\Leftrightarrow-5x+2=2-5x\)
\(\Leftrightarrow-5x+5x=2-2\)
\(\Leftrightarrow0=0\)
=>pt luôn có nghiệm với mọi x.