cho tam giác ABC có ba góc nhọn, kẻ đường cao AH a) chứng minh: sinA + cosA >1 b) chứng minh: BC = AH.(cotgB + cotgC) c) Biết AH =6cm góc B =60 độ góc C = 45 độ . tính diện tích tam giác ABC
DH
Những câu hỏi liên quan
1. Cho ∆ABC có ba góc nhọn. chứng minh sinA+ cosA> 1
Do \(0< \sin A,\cos A< 1\) (vì tam giác ABC có 3 góc nhọn) nên ta có điều dưới đây:
\(\sin A>\sin^2A\)
\(\cos A>\cos^2A\)
\(\Rightarrow\sin A+\cos A>\sin^2A+\cos^2A=1\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có ba góc nhọn, đường cao AH. Ở miền ngoài của tam giác ABC vẽ các tam giác vuông cân ABE và tam giác ACF đều nhận A làm đỉnh góc vuông. Kẻ EM, FN cùng vuông góc với AH (M, N thuộc AH).
a. Chứng minh rằng: EM + HC = NH
b. Chứng minh rằng: EN // FM
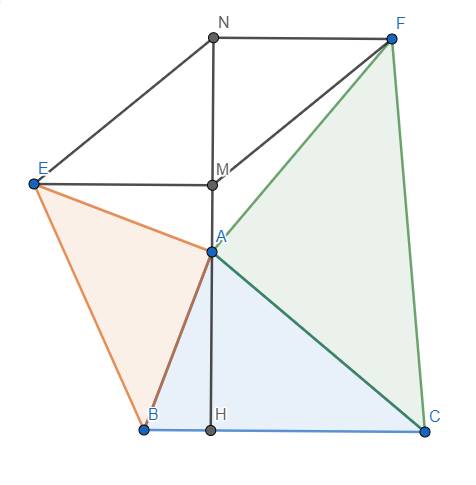
a) Do tam giác AEB vuông cân tại A nên \(\left\{{}\begin{matrix}\widehat{EAB}=90^o\\AE=AB\end{matrix}\right.\)
Ta thấy \(\widehat{MEA}=\widehat{BAH}\) vì chúng cùng phụ với \(\widehat{EAM}\)
Xét 2 tam giác HAB vuông tại H và MEA vuông tại M, ta có:
\(AE=AB\left(cmt\right),\widehat{MEA}=\widehat{BAH}\left(cmt\right)\)
\(\Rightarrow\Delta HAB=\Delta MEA\left(ch-gn\right)\) \(\Rightarrow AH=ME\) (1)
Tương tự, ta cũng có \(\Delta HAC=\Delta NFA\Rightarrow HC=AN\) (2)
Từ (1) và (2) suy ra \(EM+HC=AH+AN\) hay \(EM+HC=HN\) (đpcm)
b) Từ \(\Delta HAC=\Delta NFA\Rightarrow AH=NF\)
Từ đó suy ra \(ME=NF\left(=AH\right)\)
Xét tam giác MNE và NMF, ta có:
\(ME=NF\left(cmt\right),\widehat{EMN}=\widehat{FNM}\left(=90^o\right)\), MN là cạnh chung.
\(\Rightarrow\Delta MNE=\Delta NMF\left(c.g.c\right)\)
\(\Rightarrow\widehat{ENM}=\widehat{FMN}\) \(\Rightarrow\) EN//FM (2 góc so le trong bằng nhau)
Ta có đpcm.
Đúng 4
Bình luận (0)
cho tam giác ABC có 3 góc nhọn, kẻ đường cao AH. Chứng minh sin A + cos A > 1
Cho tam giác ABC có 3 góc nhọn. Gọi AH là đường cao lớn nhất trong ba đường cao. BE là trung tuyến kẻ từ đỉnh B. Cho biết AH=BE.
a) Chứng minh: góc CBE = 30 độ
b) Chứng minh: góc ABC < hoặc = 60 độ.
c) Tam giác ABC thoả mãn điều kiện gì thì góc B= 60 độ.
Cho tam giác abc có ba góc nhọn nội tiếp đường tròn tâm O kẻ đường thẳng (d) tiếp tuyến với đường tròn tâm O(với C là tiếp điểm ) AH, BK là đường cao của tam giác ABC a) Chứng minh tứ giác AKHB nội tiếp b) Chứng minh KHvuông góc với OC2)từ A,H,B,K lần lượt kẻ các đường thẳng song song với OC cắt đường thẳng (d) theo thứ tự là M,N,E,F:a)chứng minh góc CAH góc CEK b) chưng minh EFMN
Đọc tiếp
Cho tam giác abc có ba góc nhọn nội tiếp đường tròn tâm O kẻ đường thẳng (d) tiếp tuyến với đường tròn tâm O(với C là tiếp điểm ) AH, BK là đường cao của tam giác ABC a) Chứng minh tứ giác AKHB nội tiếp b) Chứng minh KHvuông góc với OC2)từ A,H,B,K lần lượt kẻ các đường thẳng song song với OC cắt đường thẳng (d) theo thứ tự là M,N,E,F:a)chứng minh góc CAH = góc CEK b) chưng minh EF=MN
Lời giải:
a)
Theo tính chất tiếp tuyến thì
Do đó tứ giác nội tiếp.
b) Vì nên (hai góc đồng vị)
Mặt khác theo tính chất hai tiếp tuyến cắt nhau ta dễ thấy là đường phân giác của góc
Do đó:
Từ
Đúng 1
Bình luận (5)
cho tam giác nhọn ABC chứng minh; sinA+cosA>1
ta có (sinA + cosA )*2 = sinA*2+cosA *2 + 2sinAcosA = 1+ 2sinAcosA > 1 .
Vì A là gọc nhọn nên sinA hay CosA > 0 ,
Đúng 0
Bình luận (0)
cho tam giác ABC có ba góc nhọn đường cao AH. Ở miền ngoài của tam giác ABC vẽ tam giác vuông cân ABE và ACF đều nhận A làm đỉnh góc vuông . Kẻ EM FN cùng vuông góc với AH(M và N thuộc AH)
a/ chứng minh :EM+HC=NH
b/ chứng minh : EN//FM
Cho tam giác ABC có ba góc nhọn và ABAC. Tam giác ABC nội tiếp đường tròn (O;R). Đường cao AH của tam giác ABC cắt đường tròn (O;R) tại điểm thứ hai là D. Kẻ DM vuông góc với AB tại M.a) Chứng minh tứ giác BDHM nội tiếp đường tròn.b) Chứng minh DA là tia phân giác của widehat{MDC}c) Gọi N là hình chiếu vuông góc của D lên đường thẳng AC, chứng minh ba điểm M, H, N thẳng hàng.d) Chứng minh AB^2+AC^2+CD^2+BD^28R^2
Đọc tiếp
Cho tam giác ABC có ba góc nhọn và AB>AC. Tam giác ABC nội tiếp đường tròn (O;R). Đường cao AH của tam giác ABC cắt đường tròn (O;R) tại điểm thứ hai là D. Kẻ DM vuông góc với AB tại M.
a) Chứng minh tứ giác BDHM nội tiếp đường tròn.
b) Chứng minh DA là tia phân giác của \(\widehat{MDC}\)
c) Gọi N là hình chiếu vuông góc của D lên đường thẳng AC, chứng minh ba điểm M, H, N thẳng hàng.
d) Chứng minh \(AB^2+AC^2+CD^2+BD^2=8R^2\)
a: góc BHD+góc BMD=180 độ
=>BHDM nội tiếp
b: BHDM nội tiếp
=>góc HDM+góc HBM=180 độ
=>góc ADM=góc ABC
=>góc ADM=góc ADC
=>DA là phân giáccủa góc MDC
c: Xét tứ giác DHNC có
góc DHC=góc DNC=90 độ
=>DHNC nội tiếp
=>góc NHD=góc NDC
góc NHD+góc MHD
=180 độ-góc NCD+góc MBD
=180 độ+180 độ-góc ABD-góc ACD
=180 độ
=>M,H,N thẳng hàng
Đúng 0
Bình luận (0)
Cho ΔABC có ba góc nhọn, kẻ đường cao AH.
a ) Chứng minh : sinA + cosA > 1.
b ) Chứng minh : BC = AH.(cotgB + cotgC).
c ) Biết AH = 6cm, góc B = 600, góc C = 450. Tính diện tích ΔABC
a) Kẻ đg cao BD của ΔABC
+ \(sinA+cosA=\frac{BD}{AB}+\frac{AD}{AB}=\frac{BD+AD}{AB}>1\)
b) \(AH.\left(cotB+cotC\right)=AH\left(\frac{BH}{AH}+\frac{CH}{AH}\right)\)
\(=AH\cdot\frac{BH+CH}{AH}=BC\)
c) + \(BC=AH\cdot\left(cotB+cotC\right)=6\cdot\left(cot60^o+cot45^o\right)\)
\(=6\cdot\left(\frac{1}{\sqrt{3}}+1\right)=2\sqrt{3}+6\)
Diện tích ΔABC là :
\(\frac{1}{2}\cdot AH\cdot BC=3\cdot\left(2\sqrt{3}+6\right)=6\sqrt{3}+18\approx28.39\left(cm^2\right)\)
Đúng 0
Bình luận (0)




